高中物理平抛运动计算题

如图所示，一小球从A点以某一水平向右的初速度出发，沿水平直线轨道运动到B点后，进入半径的光滑竖直圆形轨道，圆形轨道间不相互重叠，即小球离开圆形轨道后可继续向C点运动，C点右侧有一壕沟，C、D两点的竖直高度，水平距离，水平轨道AB长为，BC长为，小球与水平轨道间的动摩擦因数，重力加速度.求：

（1）若小球恰能通过圆形轨道的最高点，求小球在A点的初速度？
（2）若小球既能通过圆形轨道的最高点，又不掉进壕沟，求小球在A点的初速度的范围是多少？

如图所示，一质点做平抛运动先后经过A、B两点，到达A点时速度方向与水平方向的夹角为30°，到达B点时速度方向与水平方向的夹角为60°．

（1）求质点在A、B位置的竖直分速度大小之比；
（2）设质点的位移s_AB与水平方向的夹角为θ，求tan θ的值．

消防车的供水系统主要由水泵、输水管道和水炮组成。如图所示，消防水炮离地高度为H，建筑物上的火点离地高度为h，水炮与火点的水平距离为x，水泵的功率为P，整个供水系统的效率η=0.6。假设水从水炮水平射出，其中水泵、输水管道没有画出，水泵放置于地面，不计空气阻力，取g=10m/s²。

（1）、若H=80m，h=60m，水炮出水速度v₀=30m/s，试求水炮与起火建筑物之间的水平距离x；
（2）、在（1）问中，若水炮每秒出水量m₀="60" kg，试求水泵的功率P；
（3）、当完成高层灭火后，还需要对散落在火点正下方地面上的燃烧物进行灭火，将水炮竖直下移至H´=45m，假设供水系统的效率η不变，水炮出水口的横截面积不变，水泵功率应调整为P´，则P´应为多大？

如图所示，一根长为L＝5m的轻绳一端固定在 O′点，另一端系一质量m=1kg的小球（小球可视为质点）。将轻绳拉至水平并将小球由位置A静止释放，小球运动到最低点O时，轻绳刚好被拉断。O点下方有一以O点为圆心，半径的圆弧状的曲面，已知重力加速度为 g＝10m／s²，求：

（1）轻绳所能承受的最大拉力F_m的大小；
（2）小球从O点运动到曲面的时间t；
（3）小球落至曲面上的动能E_k。

宇航员在一星球表面上的某高处，沿水平方向抛出一个小球，经时间t，小球落到星球表面，测出抛出点与落地点之间距离为L。若抛出时的初速增大到原来的2倍，则抛出点到落地点间的距离为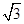L。已知两落地点在同一水平面上，该星球的质量M，万有引力常数为G，求:
（1）该星球的半径R。 
（2）该星球上的第一宇宙速度。

在我国南方农村地区有一种简易水轮机，如图所示，从悬崖上流出的水可看做连续做平抛运动的物体，水流轨道与下边 放置的轮子边缘相切，水冲击轮子边缘上安装的挡水板，可使轮子连续转动，输出动力．当该系统工作稳定时，可近似认为水的末速度与 轮子边缘的线速度相同．设水的流出点比轮轴高h＝5.6 m，轮子半径  R＝1 m．调整轮轴O的位置，使水流与轮边缘切点对应的半径与水平线成θ＝37°角．(已知sin 37°＝0.6，cos 37°＝0.8，g＝10 m/s²)问：

（1）水流的初速度v₀大小为多少？
（2）若不计挡水板的大小，则轮子转动的角速度为多少？

因为手边没有天平，小王同学思考如何利用一已知劲度系数为k的弹簧和长度测量工具来粗测一小球的质量，他从资料上查得弹簧的弹性势能 (其中x为弹簧形变量)后，设计了如下实验:将弹簧一端固定在水平桌面上，另一端紧靠小球，弹簧原长时小球恰好在桌边，然后压缩弹簧并测得压缩量x，释放弹簧，小球飞出后落在水平地面上，测出桌高h以及落点到桌边沿的水平距离s．

（1）小球质量的表达式为:  ．
（2）如果桌面摩擦是本次实验误差的主要因素，那么小球质量的测量值将  (填“偏大”、“偏小”或“准确”)．

(16分)如图所示，ABDO是处于竖直平面内的光滑轨道，AB是半径R＝15m的四分之一圆周轨道，半径OA处于水平位置，BDO是直径为15m的半圆轨道，D为BDO轨道的中央，一个小球P从A点的正上方距水平半径OA高H处自由落下，沿竖直平面内的轨道通过D点时对轨道的压力等于其重力的倍，试求：

⑴高度H的大小；
⑵讨论此球能否到达BDO轨道的O点，并说明理由；
⑶小球沿轨道运动后再次落到轨道上的速度的大小和方向。

(15分)在一次国际城市运动会中，要求运动员从高为H的平台上A点，由静止出发，沿着动摩擦因数为μ的滑道向下运动到B点后水平滑出，最后落在水池中，如图所示，设滑道的水平距离为L，B点的高度h可由运动员自由调节(取g＝10m/s²)，求：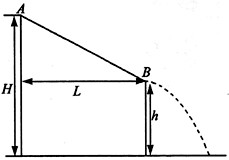

⑴运动员到达B点的速度与高度h的关系；
⑵运动员要达到最大水平运动距离，B点的高度h应调为多大？对应的最大水平距离s_max为多少？
⑶若图中H＝4m，L＝5m，动摩擦因数μ＝0.2，则水平运动距离要达到7m，h值应为多少？

如图所示为跳台滑雪的示意图。一名运动员在助滑路段取得高速后从a点以水平初速度v₀=15m/s飞出，在空中飞行一段距离后在b点着陆。若测得ab两点的高度差h=20m，不计空气阻力，g取10m/s²，求：

（1）运动员在空中飞行的时间；
（2）运动员在b点着陆前瞬间速度的大小。

(12分)如图所示，水平桌面上有一轻弹簧，左端固定在A点，自然状态时其右端位于B点。水平桌面右侧有一竖直放置的轨道MNP，其形状为半径R＝1.0m圆环剪去了左上角120°的圆弧，MN为其竖直直径，P点到桌面的数值距离是h＝2.4m。用质量m₁＝0.4kg的物块将弹簧缓慢压缩到C点，释放后弹簧恢复原长时物块恰停止在B点，用同种材料、质量为m₂＝0.2kg的物块将弹簧缓慢压缩到C点释放，物块通过B点后做匀变速运动，其位移与时间的关系为x＝6t－2t²，物块飞离桌面后恰好由P点沿切线落入圆轨道(不计空气阻力，g取10m/s²)。求：

⑴物块m₂过B点时的瞬时速度v_B及与桌面间的滑动摩擦因数μ；
⑵若轨道MNP光滑，物块m₂经过轨道最低点N时对轨道的压力F_N；＝×－·
⑶若物块m₂刚好能到达轨道最高点M，则释放m₂后整个运动过程中其克服摩擦力做的功W。

如图所示，半径R＝1.0m的光滑圆弧轨道固定在竖直平面内，轨道的一个端点B和圆心O的连线与水平方向间的夹角θ＝37°，另一端点C为轨道的最低点。C点右侧的水平路面上紧挨C点放置一木板，木板质量M＝2kg，上表面与C点等高。质量m＝1kg的物块(可视为质点)从空中A点以v₀＝1.2m/s的速度水平抛出，恰好从轨道的B端沿切线方向进入轨道。已知物块与木板间的动摩擦因数μ₁＝0.2，木板与路面间的动摩擦因数μ₂＝0.08，取g＝10 m/s²，。试求：

（1）物块经过轨道上的C点时对轨道的压力大小；
（2）若物块刚好滑到木板的中点停止，求木板的长度。

如图所示，遥控赛车比赛中一个规定项目是“飞跃壕沟”，比赛要求：赛车从起点出发，沿水平直轨道运动，在B点飞出后越过“壕沟”，落在平台EF段。已知赛车的额定功率=10.0W，赛车的质量m=1.0kg，在水平直轨道上受到的阻力f=2.0N，AB段长L=10.0m，BE的高度差h=1.25m，BE的水平距离x=1.5m。若赛车车长不计，忽略空气阻力，g取10m/s²．

（1）若赛车在水平直轨道上能达到最大速度，求最大速度v_m的大小；
（2）要越过壕沟，求赛车在B点最小速度v的大小；
（3）若在比赛中赛车通过A点时速度v_A=1m/s，且赛车达到额定功率。要使赛车完成比赛，求赛车在AB段通电的最短时间t．

如图所示，水平光滑轨道AB与竖直半圆形光滑轨道在B点平滑连接，AB段长x=10m，半圆形轨道半径R=2.5m。质量m=0.10kg的小滑块（可视为质点）在水平恒力F作用下，从A点由静止开始运动，经B点时撤去力F，小滑块进入半圆形轨道，沿轨道运动到最高点C，从C点水平飞出。重力加速度g取10m/s²。

（1）若小滑块从C点水平飞出后又恰好落在A点。滑块落回A点时的速度；
（2）如果要使小滑块在圆弧轨道运动过程中不脱离轨道，求水平恒力F应满足的条件。

如图，一个质量为0.6kg 的小球以某一初速度从P点水平抛出，恰好从光滑圆弧ABC的A点的切线方向进入圆弧（不计空气阻力，进入圆弧时无机械能损失）。已知圆弧的半径R=0.3m，θ=60°，小球到达A点时的速度 v_A="4" m/s 。取g ="10" m/s²，求：

（1）小球做平抛运动的初速度v₀；
（2）P点与A点的高度差；
（3）小球到达圆弧最高点C时对轨道的压力。