因为手边没有天平,小王同学思考如何利用一已知劲度系数为k的弹簧和长度测量工具来粗测一小球的质量,他从资料上查得弹簧的弹性势能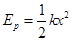 (其中x为弹簧形变量)后,设计了如下实验:将弹簧一端固定在水平桌面上,另一端紧靠小球,弹簧原长时小球恰好在桌边,然后压缩弹簧并测得压缩量x,释放弹簧,小球飞出后落在水平地面上,测出桌高h以及落点到桌边沿的水平距离s.
(其中x为弹簧形变量)后,设计了如下实验:将弹簧一端固定在水平桌面上,另一端紧靠小球,弹簧原长时小球恰好在桌边,然后压缩弹簧并测得压缩量x,释放弹簧,小球飞出后落在水平地面上,测出桌高h以及落点到桌边沿的水平距离s.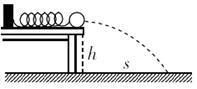
(1)小球质量的表达式为: .
(2)如果桌面摩擦是本次实验误差的主要因素,那么小球质量的测量值将 (填“偏大”、“偏小”或“准确”).
因为手边没有天平,小王同学思考如何利用一已知劲度系数为k的弹簧和长度测量工具来粗测一小球的质量,他从资料上查得弹簧的弹性势能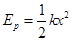 (其中x为弹簧形变量)后,设计了如下实验:将弹簧一端固定在水平桌面上,另一端紧靠小球,弹簧原长时小球恰好在桌边,然后压缩弹簧并测得压缩量x,释放弹簧,小球飞出后落在水平地面上,测出桌高h以及落点到桌边沿的水平距离s.
(其中x为弹簧形变量)后,设计了如下实验:将弹簧一端固定在水平桌面上,另一端紧靠小球,弹簧原长时小球恰好在桌边,然后压缩弹簧并测得压缩量x,释放弹簧,小球飞出后落在水平地面上,测出桌高h以及落点到桌边沿的水平距离s.
(1)小球质量的表达式为: .
(2)如果桌面摩擦是本次实验误差的主要因素,那么小球质量的测量值将 (填“偏大”、“偏小”或“准确”).