假定平面内的一条直线将该平面内的一个区域分成面积相等的两个区域,则称这条直线平分这个区域.如图, 是平面
是平面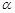 内的任意一个封闭区域.现给出如下结论:
内的任意一个封闭区域.现给出如下结论:
① 过平面内的任意一点至少存在一条直线平分区域 ;
;
② 过平面内的任意一点至多存在一条直线平分区域 ;
;
③ 区域 内的任意一点至少存在两条直线平分区域
内的任意一点至少存在两条直线平分区域 ;
;
④ 平面内存在互相垂直的两条直线平分区域 成四份.
成四份.
其中正确结论的序号是 .
已知双曲线 的离心率为2,有一个焦点与抛物线
的离心率为2,有一个焦点与抛物线 的焦点重合,则
的焦点重合,则 __________.
__________.
将一张边长为12cm的纸片按如图1所示阴影部分裁去四个全等的等腰三角形,将余下部分沿虚线折成一个有底的正四棱锥模型,如图2放置.若正四棱锥的正视图是正三角形(如图3),则四棱锥的体积是___________ .
.
从54张扑克牌中抽出一张,抽到的扑克牌为梅花的概率为________, 抽到的扑克牌为K的条件下恰好是梅花的概率为_________.
设函数 ,其中
,其中 .若
.若 对任意
对任意 恒成立,则正数
恒成立,则正数 的最小值为_________,此时,
的最小值为_________,此时, =____________.
=____________.