已知函数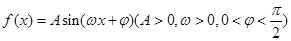 部分图象如图所示。
部分图象如图所示。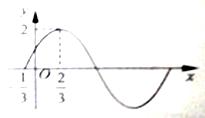
(1)求函数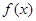 的解析式;
的解析式;
(2)当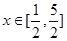 时,求函数
时,求函数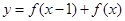 的值域。
的值域。
如图,在平面直角坐标系 中,离心率为
中,离心率为 的椭圆
的椭圆
 的左顶点为
的左顶点为 ,过原点
,过原点 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆 交于
交于 两点,直线
两点,直线 分别与
分别与 轴交于
轴交于 两点.若直线
两点.若直线 斜率为
斜率为 时,
时, .
.
(1)求椭圆 的标准方程;
的标准方程;
(2)试问以 为直径的圆是否经过定点(与直线
为直径的圆是否经过定点(与直线 的斜率无关)?请证明你的结论.
的斜率无关)?请证明你的结论.
(本小题满分16分)
在平面直角坐标系 中,已知椭圆
中,已知椭圆 :
: 的离心率
的离心率 ,直线
,直线 过椭圆
过椭圆 的右焦点
的右焦点 ,且交椭圆
,且交椭圆 于
于 ,
, 两点.
两点.
(1)求椭圆 的标准方程;
的标准方程;
(2)已知点 ,连结
,连结 ,过点
,过点 作垂直于
作垂直于 轴的直线
轴的直线 ,设直线
,设直线 与直线
与直线 交于点
交于点 ,试探索当
,试探索当 变化时,是否存在一条定直线
变化时,是否存在一条定直线 ,使得点
,使得点 恒在直线
恒在直线 上?若存在,请求出直线
上?若存在,请求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分12分)在 中,角
中,角 ,
, ,
, 所对的边分别为
所对的边分别为 ,
, ,
, ,且满足
,且满足 .
.
(1)求角 的大小;
的大小;
(2)已知 ,
, 的面积为
的面积为 ,求边长
,求边长 的值.
的值.
(本小题满分13分)我国东部某风景区内住着一个少数民族部落,该部落拟投资 万元用于修复和加强民俗文化基础设施.据测算,修复好部落民俗文化基础设施后,任何一个月(每月均按
万元用于修复和加强民俗文化基础设施.据测算,修复好部落民俗文化基础设施后,任何一个月(每月均按 天计算)中第
天计算)中第 天的游客人数
天的游客人数 近似满足
近似满足 (单位:千人),第
(单位:千人),第 天游客人均消费金额
天游客人均消费金额 近似满足
近似满足 (单位:元).
(单位:元).
(1)求该部落第 天的日旅游收入
天的日旅游收入 (单位:千元,
(单位:千元, ,
, )的表达式;
)的表达式;
(2)若以一个月中最低日旅游收入金额的 %作为每一天应回收的投资成本,试问该部落至少经过几年就可以收回全部投资成本.
%作为每一天应回收的投资成本,试问该部落至少经过几年就可以收回全部投资成本.
函数
(Ⅰ)求 的值域和单调递减区间;
的值域和单调递减区间;
(Ⅱ)在 中角
中角 所对的边分别是
所对的边分别是 ,且
,且 ,
, ,
, ,求
,求 的面积。
的面积。
(本小题满分10分)选修4-1:几何证明选讲
已知 (
( )的外接圆为圆
)的外接圆为圆 ,过
,过 的切线
的切线 交
交 于点
于点 ,过
,过 作直线交
作直线交 于点
于点 ,且
,且

(1)求证: 平分角
平分角 ;
;
(2)已知 ,求
,求 的值.
的值.
(本小题满分12分)在平行六面体 中,
中, ,
, ,
, 是
是 的中点.
的中点.
(1)证明 面
面 ;
;
(2)当平面 平面
平面 ,求
,求 .
.
(本小题满分13分)如图所示的“8”字形曲线是由两个关于 轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是
轴对称的半圆和一个双曲线的一部分组成的图形,其中上半个圆所在圆方程是 ,双曲线的左、右顶点
,双曲线的左、右顶点 、
、 是该圆与
是该圆与 轴的交点,双曲线与半圆相交于与
轴的交点,双曲线与半圆相交于与 轴平行的直径的两端点.
轴平行的直径的两端点.
(1)试求双曲线的标准方程;
(2)记双曲线的左、右焦点为 、
、 ,试在“8”字形曲线上求点
,试在“8”字形曲线上求点 ,使得
,使得 是直角.
是直角.
(本小题满分12分)“ALS冰桶挑战赛”是一项社交网络上发起的筹款活动,活动规定:被邀请者要么在24小时内接受挑战,要么选择为慈善机构捐款(不接受挑战),并且不能重复参加该活动.若被邀请者接受挑战,则他需在网络上发布自己被冰水浇遍全身的视频内容,然后便可以邀请另外3个人参与这项活动.假设每个人接受挑战与不接受挑战是等可能的,且互不影响.
(Ⅰ)若某被邀请者接受挑战后,对其他3个人发出邀请,则这3个人中至少有2个人接受挑战的概率是多少?
(Ⅱ)假定(Ⅰ)中被邀请到的3个人中恰有两人接受挑战.根据活动规定,现记 为接下来被邀请到的6个人中接受挑战的人数,求
为接下来被邀请到的6个人中接受挑战的人数,求 的分布列和均值(数学期望).
的分布列和均值(数学期望).
本题共有2个小题,第1小题满分6分,第2小题满分6分)
在 中,
中, 分别为内角
分别为内角 所对的边,且满足
所对的边,且满足 ,
, .
.
(1)求 的大小;
的大小;
(2)若 ,
, ,求
,求 的面积.
的面积.
(本小题满分12分)已知数列 是公差不为
是公差不为 的等差数列,
的等差数列,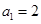 ,且
,且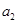 ,
, ,
,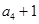 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列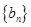 的前
的前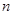 项和
项和 .
.