已知变换T是将平面内图形投影到直线y=2x上的变换,求它所对应的矩阵.
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为 ,中奖可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率.
,中奖可以得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为X,求X≤3的概率.
如图,渔船甲位于岛屿A的南偏西60°方向的B处,且与岛屿A相距12海里,渔船乙以10海里/时的速度从岛屿A出发沿正北方向航行,若渔船甲同时从B处出发沿北偏东α的方向追赶渔船乙,刚好用2小时追上,此时到达C处.
(1)求渔船甲的速度;
(2)求sinα的值.
已知数列 的前
的前 项和为
项和为 ,且2
,且2 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 求数列
求数列 的前
的前 项和
项和 .
.
某校高三年级一次数学考试后,为了解学生的数学学习情况,随机抽取 名学生的数学成绩,制成表所示的频率分布表.
名学生的数学成绩,制成表所示的频率分布表.
| 组号 |
分组 |
频数 |
频率 |
| 第一组 |
 |
 |
 |
| 第二组 |
 |
 |
 |
| 第三组 |
 |
 |
 |
| 第四组 |
 |
 |
 |
| 第五组 |
 |
 |
 |
| 合计 |
 |
 |
(1)求 、
、 、
、 的值;
的值;
(2)若从第三、四、五组中用分层抽样方法抽取 名学生,并在这
名学生,并在这 名学生中随机抽取
名学生中随机抽取 名学生与张老师面谈,求第三组中至少有
名学生与张老师面谈,求第三组中至少有 名学生与张老师面谈的概率
名学生与张老师面谈的概率
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
| 日期 |
12月1日 |
12月2日 |
12月3日 |
12月4日 |
12月5日 |
| 温差x/℃ |
10 |
11 |
13 |
12 |
8 |
| 发芽数y /颗 |
23 |
25 |
30 |
26 |
16 |
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程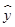 =bx+a;
=bx+a;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
一个车间为了规定工时定额.需要确定加工零件所花费的时间,为此进行了10次试验.测得的数据如下:
| 零件数x/个 |
10 |
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |
| 加工时间y/分 |
62 |
68 |
75 |
81 |
89 |
95 |
102 |
108 |
115 |
122 |
(1)y与x是否具有线性相关关系?
(2)如果y与x具有线性相关关系,求回归直线方程;
(3)根据求出的回归直线方程,预测加工200个零件所用的时间为多少?