若直线ax﹣by+2=0(a>0,b>0)被圆x2+y2+2x﹣4y+1=0截得的弦长为4,则 的最小值为( )
的最小值为( )
A. |
B.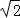 |
C.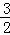 + +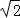 |
D.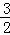 +2 +2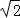 |
如图,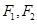 是双曲线
是双曲线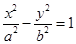
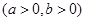 的左、右焦点,过
的左、右焦点,过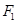 的直线
的直线 与双曲线的左右两支分别交于点
与双曲线的左右两支分别交于点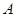 、
、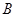 .若
.若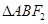 为等边三角形,则双曲线的离心率为( )
为等边三角形,则双曲线的离心率为( )
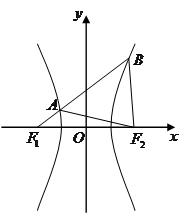
| A.4 | B.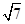 |
C.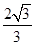 |
D.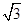 |
若存在实常数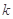 和
和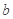 ,使得函数
,使得函数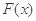 和
和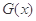 对其公共定义域上的任意实数
对其公共定义域上的任意实数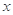 都满足:
都满足: 和
和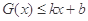 恒成立,则称此直线
恒成立,则称此直线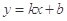 为
为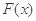 和
和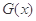 的“隔离直线”,已知函数
的“隔离直线”,已知函数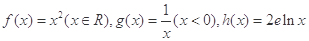 ,有下列命题:
,有下列命题:
①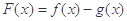 在
在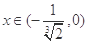 内单调递增;
内单调递增;
②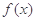 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且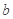 的最小值为
的最小值为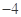 ;
;
③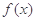 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且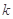 的取值范围是
的取值范围是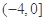 ;
;
④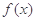 和
和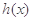 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线”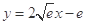 .
.
其中真命题的个数有( )
A.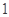 个 个 |
B.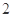 个 个 |
C.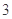 个 个 |
D.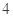 个 个 |
若曲线f(x,y)=0上两个不同点处的切线重合,则称这条切线为曲线f(x,y)=0的“自公切线”.下列方程:①x2-y2=1;②y=x2-|x|;③y=3sin x+4cos x;④|x|+1=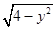 对应的曲线中存在“自公切线”的有 ( )
对应的曲线中存在“自公切线”的有 ( )
| A.①② | B.②③ | C.①④ | D.③④ |
如图,将平面直角坐标系中的纵轴绕原点 顺时针旋转
顺时针旋转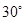 后,构成一个斜坐标平面
后,构成一个斜坐标平面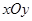 .在此斜坐标平面
.在此斜坐标平面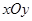 中,点
中,点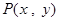 的 坐标定义如下:过点
的 坐标定义如下:过点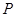 作两坐标轴的平行线,分别交两轴于
作两坐标轴的平行线,分别交两轴于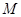 、
、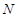 两点,则
两点,则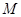 在
在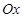 轴上表示的数为
轴上表示的数为 ,
,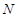 在
在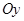 轴上表示的数为
轴上表示的数为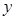 .那么以原点
.那么以原点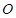 为圆心的单位圆在此斜坐标系下的方程为
为圆心的单位圆在此斜坐标系下的方程为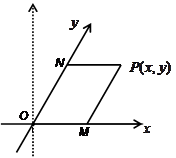
A.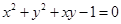 |
B.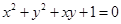 |
C.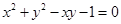 |
D.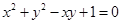 |
如图,在Rt△ABC中,∠ABC=90°,AB=BC.点D是线段AB上的一点,连结CD,过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF.给出以下四个结论:
① ;
;
②若点D是AB的中点,则AF=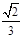 AB;
AB;
③当B、C、F、D四点在同一个圆上时,DF=DB;
④若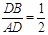 ,则
,则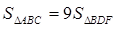 .
.
其中正确的结论序号是( )
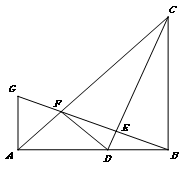
A.①② B.③④ C.①②③ D.①②③④