河南省信阳高中高二上12月月考文科数学试卷
已知x∈R,则“x2﹣3x<0”是“(x﹣1)(x﹣2)≤0成立”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
公比为2的等比数列{an}的各项都是正数,且a3a11=16,则a5=( )
| A.1 | B.2 | C.4 | D.8 |
给出如下四个命题:
①若“p且q”为假命题,则p、q均为假命题;
②命题“若a>b,则2a>2b﹣1”的否命题为“若a≤b,则2a≤2b﹣1”;
③“∀x∈R,x2+1≥1”的否定是“∃x∈R,x2+1≤1;
④在△ABC中,“A>B”是“sinA>sinB”的充要条件.
其中不正确的命题的个数是( )
| A.4 | B.3 | C.2 | D.1 |
数列{an}为等差数列,a1,a2,a3为等比数列,a5=1,则a10=( )
| A.5 | B.﹣1 | C.0 | D.1 |
已知点P是以F1,F2为焦点的双曲线 =1(a>0,b>0)上一点,
=1(a>0,b>0)上一点, =0,tan∠PF1F2=
=0,tan∠PF1F2= ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A. |
B.2 | C. |
D. |
在△ABC中,若A=60°,BC=4 ,AC=4
,AC=4 ,则角B的大小为( )
,则角B的大小为( )
| A.30° | B.45° | C.135° | D.45°或135° |
△ABC的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且c=2a,则cosB=( )
A. B.
B. C.
C. D.
D.
已知直线y=﹣x+1与椭圆 +
+ =1(a>b>0)相交于A、B两点,若椭圆的离心率为
=1(a>b>0)相交于A、B两点,若椭圆的离心率为 ,焦距为2,则线段AB的长是( )
,焦距为2,则线段AB的长是( )
A.
 B.
B.
 C.
C. D.2
D.2
若直线ax﹣by+2=0(a>0,b>0)被圆x2+y2+2x﹣4y+1=0截得的弦长为4,则 的最小值为( )
的最小值为( )
A. |
B.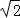 |
C.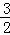 + +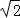 |
D.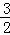 +2 +2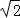 |
设抛物线y2=8x的准线与x轴交于点Q,若过点Q的直线l与抛物线有公共点,则直线l的斜率的取值范围是( )
A.[﹣ , , ] ] |
B.[﹣2,2] |
| C.[﹣1,1] | D.[﹣4,4] |
数列{an}的通项公式是an=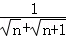 ,若前n项和为10,则项数n为( )
,若前n项和为10,则项数n为( )
| A.11 | B.99 | C.120 | D.121 |
已知点P(1,0)到双曲线C: (a>0,b>0)的一条渐近线的距离为
(a>0,b>0)的一条渐近线的距离为 ,则双曲线C的离心率为 .
,则双曲线C的离心率为 .
已知函数f(x)=x2+xlnx.
(1)求f′(x);
(2)求函数f(x)图象上的点P(1,1)处的切线方程.
已知命题p:“存在 ”,命题q:“曲线
”,命题q:“曲线 表示焦点在x轴上的椭圆”,命题s:“曲线
表示焦点在x轴上的椭圆”,命题s:“曲线 表示双曲线”
表示双曲线”
(1)若“p且q”是真命题,求m的取值范围;
(2)若q是s的必要不充分条件,求t的取值范围.
设函数f(x)=ax2+(b﹣2)x+3(a≠0)
(1)若不等式f(x)>0的解集(﹣1,3).求a,b的值;
(2)若f(1)=2,a>0,b>0求 +
+ 的最小值.
的最小值.
已知数列{an}的各项均为正数,Sn是数列{an}的前n项和,且4Sn=an2+2an﹣3.
(1)求数列{an}的通项公式;
(2)已知bn=2n,求Tn=a1b1+a2b2+…+anbn的值.
已知△ABC中,角A,B,C所对的边分别是a,b,c,且2(a2+b2﹣c2)=3ab;
(1)求 ;
;
(2)若c=2,求△ABC面积的最大值.
 ,则z=2x﹣y的最大值是( )
,则z=2x﹣y的最大值是( )
 的焦点坐标是 .
的焦点坐标是 . ,则角C= .
,则角C= . 的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离最小值为
的左焦点F为圆x2+y2+2x=0的圆心,且椭圆上的点到点F的距离最小值为 .
. +y2=1;
+y2=1; ),证明:
),证明: 为定值.
为定值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号