高中数学表面展开图试题

如图，正方体ABCD－A′B′C′D′的棱长为4，动点E，F在棱AB上，且EF＝2，动点Q在棱D′C′上，则三棱锥A′－EFQ的体积 （）

A．与点E，F位置有关

B．与点Q位置有关

C．与点E，F，Q位置都有关

D．与点E，F，Q位置均无关，是定值

一个三棱锥的侧棱长都相等，底面是正三角形，其正（主）视图如右图所示．该三棱锥侧面积和体积分别是（）

A．	B．
C．	D．

一个几何体的三视图如图所示，则该几何体的体积是________．

某几何体的三视图如图所示，则该几何体中，面积最大的侧面积的面积为（）

A．

B．

C．

D．3

如图，在等腰梯形中，，，为的中点，将和分别沿向上折起，使重合于点，则三棱锥的外接球的体积为（）．

A．

B．

C．

D．

如图是一个无盖器皿的三视图，正视图、侧视图和俯视图中的正方形边长为2，正视图、侧视图中的虚线都是半圆，则该器皿的表面积是（）

A．π+24

B．π+20

C．2π+24

D．2π+20

已知在直角梯形ABCD中，，将直角梯形ABCD沿AC折叠成三棱锥D-ABC，当三棱锥D-ABC的体积取最大值时，其外接球的体积为 ．

如图，一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形，且直角边长为1，那么这个几何体的体积为（）

A．1

B．

C．

D．

将边长为1的正方形以其一边所在直线为旋转轴旋转一周，所得几何体的侧面积是（）

A．4π

B．3π

C．2π

D．π

一个几何体的三视图如图，则该几何体的体积是（）

A．+8

B．7+4

C．+8

D．+4

如图是某直三棱柱被削去上底后的直观图与三视图的侧视图、俯视图，在直观图中，M是BD的中点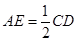，，侧视图是直角梯形，俯视图是等腰直角三角形，有关数据如图所示。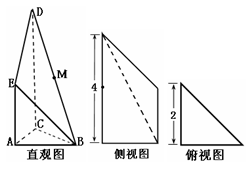

（Ⅰ）求出该几何体的体积；
（Ⅱ）试问在边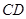上是否存在点N，使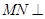平面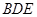？ 若存在，确定点N的位置(不需证明)；若不存在，请说明理由。

某几何体三视图如下，图中三个等腰三角形的直角边长都是，该几何体的体积为（）

A．	B．
C．	D．

正方体的棱长为，则其外接球的表面积为（）

A．

B．

C．

D．

设一个圆锥的侧面展开图是半径为的半圆，则此圆锥的体积为 ．

已知某几何体的三视图如下图所示，其正视图为矩形，侧视图为等腰直角三角形，俯视图为直角梯形．则该几何体的表面积是 ；体积是 ．