高中数学截面及其作法填空题

若命题“$x∈R,x²＋ax＋1＜0”是真命题，则实数a的取值范围为  。

若命题“$x∈R,x²＋ax＋1＜0”是真命题，则实数a的取值范围为  。

若命题“∃x∈R,2x²-3ax+9<0”为假命题,则实数a的取值范围是　　　.

设集合A={(x,y)|(x-4)²+y²=1},B={(x,y)|(x-t)²+(y-at+2)²=1}.如果命题“∃t∈R,A∩B≠”是真命题,则实数a的取值范围是　　　. 

在命题p的四种形式的命题(原命题、逆命题、否命题、逆否命题)中，正确命题的个数记为f(p)，已知命题p：“若两条直线l₁：a₁x＋b₁y＋c₁＝0，l₂：a₂x＋b₂y＋c₂＝0平行，则a₁b₂－a₂b₁＝0”．那么f(p)＝________．

已知命题p₁：函数y＝ln(x＋)，是奇函数，p₂：函数y＝为偶函数，则下列四个命题：
①p₁∨p₂；②p₁∧p₂；③(p₁)∨p₂；④p₁∧(p₂)．
其中，真命题是________．(填序号)

(1)命题“若a＞b，则2^a＞2^b－1”的否命题为____________________________；
(2)命题：“若x²＋x－m＝0没有实根，则m≤0”是____(填“真”或“假”)命题；
(3)命题p：“有些三角形是等腰三角形”，则p是____________________．

下列命题中的真命题有________．(填序号)
①x∈R，x＋＝2；
②x∈R，sinx＝－1；
③x∈R，x²>0；
④x∈R，2^x>0.

已知在实数a，b满足某一前提条件时，命题“若a＞b，则＜”及其逆命题、否命题和逆否命题都是假命题，则实数a，b应满足的前提条件是________．

若命题p：曲线－＝1为双曲线，命题q：函数f(x)＝(4－a)^x在R上是增函数，且p∨q为真命题，p∧q为假命题，则实数a的取值范围是________．

设命题p：非零向量a，b，|a|＝|b|是(a＋b)⊥(a－b)的充要条件；命题q：平面上M为一动点，A，B，C三点共线的充要条件是存在角α，使＝sin²α＋cos²α，下列命题①p∧q；②p∨q；③¬p∧q；④¬p∨q.
其中假命题的序号是________．(将所有假命题的序号都填上)

下列说法：
①“∃x∈R,2^x＞3”的否定是“∀x∈R,2^x≤3”；
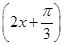②函数y＝sin sin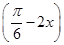的最小正周期是π；
③命题“函数f(x)在x＝x₀处有极值，则f′(x₀)＝0”的否命题是真命题；
④f(x)是(－∞，0)∪(0，＋∞)上的奇函数，x＞0时的解析式是f(x)＝2^x，则x＜0时的解析式为f(x)＝－2^－x.其中正确的说法是________．

命题“末位数字是0或5的整数能被5整除”的否定是　　　　　　　　　;它的否命题是　　　　　　　　　.

已知条件p:x²-x≥6;q:x∈Z,当x∈M时,“p且q”与“q”同时为假命题,则x取值组成的集合M=　　　　.

命题“对任意x∈R,|x-2|+|x-4|>3”的否定是　　　　.