有下列六个命题:
(1)一定存在直线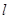 ,使函数
,使函数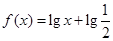 的图像与函数
的图像与函数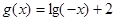 的图像关于直线
的图像关于直线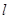 对称;
对称;
(2)直线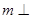 平面
平面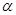 ,直线
,直线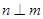 ,则
,则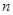 ∥
∥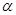 ;
;
(3)已知数列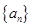 的前
的前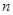 项和为
项和为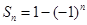 ,
,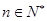 ,则数列
,则数列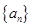 一定是等比数列;
一定是等比数列;
(4)过抛物线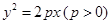 上的任意一点
上的任意一点 的切线方程一定可以表示为
的切线方程一定可以表示为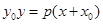 ;
;
(5)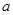 是正数,则“
是正数,则“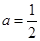 ”是“对任意正数
”是“对任意正数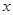 ,
,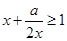 ”的充要条件;
”的充要条件;
(6)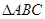 中,
中, ,则
,则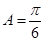 .则正确命题的个数是_______.
.则正确命题的个数是_______.
一般地,如果函数 的定义域为
的定义域为 ,值域也为
,值域也为 ,则称函数
,则称函数 为“保域函数”,下列函数是“保域函数”的有 .(填上所有正确答案的序号)
为“保域函数”,下列函数是“保域函数”的有 .(填上所有正确答案的序号)
① ; ②
; ② ;
;
③ ;④
;④ ;
;
⑤ 。
。
设集合M={f(x)|存在实数t使得函数f(x)满足f(t+1)=f(t)+f(1)},则下列函数(a,b,k都是常数):
① ;②
;② ;③
;③ ;④
;④ .
.
其中属于集合M的函数是_____(填序号).
对a,b∈R,记max(a,b)= 函数f(x)=max(|x+1|,-x2+1)的最小值是 .
函数f(x)=max(|x+1|,-x2+1)的最小值是 .
给出以下四个结论:
①函数 的对称中心是
的对称中心是
②若不等式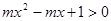 对任意的x∈R都成立,则
对任意的x∈R都成立,则 ;
;
③已知点 与点Q(l,0)在直线
与点Q(l,0)在直线 两侧,则
两侧,则 ;
;
④若将函数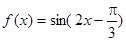 的图像向右平移
的图像向右平移 个单位后变为偶函数,则
个单位后变为偶函数,则 的最小值是
的最小值是 .
.
其中正确的结论是____________(写出所有正确结论的编号).
已知定义在区间[0,1]上的函数 图象如图所示,对于满足0<
图象如图所示,对于满足0< <
< <1的
<1的
任意 ,
, 给出下列结论:
给出下列结论:
① ②
② ③
③ ;
;
其中正确结论的序号是 .(把所有正确结论的序号都填写在横线上)
(理科)已知函数
 是非零常数,关于
是非零常数,关于 的方程
的方程 有且仅有三个不同的实数根,若
有且仅有三个不同的实数根,若 分别是三个根中的最小根和最大根,
分别是三个根中的最小根和最大根, 则
则 = .
= .
下列说法正确的为___________
①函数
 与直线
与直线 的交点个数为0或l;
的交点个数为0或l;
②集合A=  ,B={
,B={ },若B
},若B  A,则-3
A,则-3 a
a 3;
3;
③函数 与函数
与函数 的图象关于直线
的图象关于直线 对称;
对称;
④函数 的值域为R的充要条件是:
的值域为R的充要条件是: ;
;
⑤与函数 关于点(1,-1)对称的函数为
关于点(1,-1)对称的函数为 .
.
下列说法正确的为 .
①集合A=  ,B={
,B={ },若B
},若B A,则-3
A,则-3 a
a 3;
3;
②函数 与直线x=l的交点个数为0或l;
与直线x=l的交点个数为0或l;
③函数y=f(2-x)与函数y=f(x-2)的图象关于直线x=2对称;
④
 ,+∞)时,函数
,+∞)时,函数
 的值域为R;
的值域为R;
⑤与函数 关于点(1,-1)对称的函数为
关于点(1,-1)对称的函数为 (2 -x
(2 -x ).
).