高中数学不定方程和方程组填空题

用二分法求函数的一个零点，其参考数据如下：

据此数据，可得方程的一个近似解（精确到0.01）为_________.

设函数＝||＋b＋c，给出下列四个命题：
①若是奇函数，则c＝0
②b＝0时，方程＝0有且只有一个实根
③的图象关于（0，c）对称
④若b0，方程＝0必有三个实根
其中正确的命题是         （填序号）

已知关于x的方程只有一个实数解，则实数的值为        .

某公司一年购买某种货物400吨，每次都购买吨，运费为4万元/次，一年的总存储费用为万元，要使一年的总运费与总存储费用之和最小，则___    ____ 吨．

函数
 ，则函数的零点的个数有__________个

关于函数的性质，有如下四个命题：
①函数的定义域为；
②函数的值域为；
③方程有且只有一个实根；
④函数的图象是中心对称图形．
其中正确命题的序号是     ．

用二分法求函数f(x)＝3^x－x－4的一个零点，其参考数据如下：

f(1.6000)＝0.200	f(1.5875)＝0.133	f(1.5750)＝0.067
f(1.5625)＝0.003	f(1.5562)＝－0.029	f(1.5500)＝－0.060

据此数据，可得方程3^x－x－4＝0的一个近似解(精确到0.01)为________．

函数的所有零点之和为   ．

已知函数（，为常数），当时，函数有极值，若函数有且只有三个零点，则实数的取值范围是        ．

已知函数f（x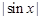）＝－kx （x≥0，k∈R）有且只有三个零点，设此三个零点中的最大值为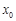，则＝      ．

定义在实数集上的函数，对一切实数x都有成立，若仅有101个不同的实数根，那么所有实数根的和为               .

定义在上的奇函数，当时，，则方程的所有解之和为        ．

已知符号表示不超过的最大整数，若函数有且仅有3个零点，则的取值范围是      ．

给出下列结论：
①函数在区间上有且只有一个零点；
②已知l是直线，是两个不同的平面．若；
③已知表示两条不同直线，表示平面．若；
④在中，已知，在求边c的长时有两解．
其中所有正确结论的序号是：           .

函数的零点个数是________．