高中数学不定方程和方程组选择题

设f（x）=3^x + 3x－8，用二分法求方程3^x + 3x－8=0在x∈（1，2）内近似解的过程中得f（1）＜0，f（1．5）＞0，f（1．25）＜0，则方程的根落在区间（  ）

A．（1．25，1．5）

B．（1，1．25）

C．（1．5，2）

D．不能确定

若函数没有零点，则的取值范围是（   ）

A．	B．
C．	D．

设，已知函数的定义域是，值域是，若函数有唯一的零点，则（  ）

A．2

B．

C．1

D．0

已知函数若互不相等，且则的取值范围是（  ）

A．

B．

C．

D．

函数的零点所在的大致区间是 (    )

A．（0，1）

B．（1，2）

C．（2，3）

D．（3，4）

已知，是互不相同的正数，且，则的取值范围是

A．

B．

C．

D．

函数f（x）＝log₃x－8＋2x的零点一定位于区间（ ）

A．（5，6）

B．（3，4）

C．（2，3）

D．（1，2）

定义域为的函数若关于的方程恰有5个不同的实数解，，，，，则等于（  ）

A．

B．

C．

D．

函数的零点个数是（   ）

A．1

B．2

C．3

D．4

已知函数有两个零点，则下列说法错误的是（   ）

A．

B．

C．

D．有极小值点，且

已知函数若存在实数b，使函数有两个零点，则a的取值范围是（  ）

A．	B．
C．	D．

定义一种新运算：a⊗b=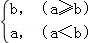，已知函数f（x）=（1+）⊗log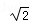x，若函数g（x）=f（x）﹣k恰有两个零点，则k的取值范围为（ ）

A．（1，2]

B．（1，2）

C．（0，2）

D．（0，1）

函数的零点个数是（    ）

A．个

B．个

C．个

D．无数个

已知函数f（x）的定义域为（﹣∞，0）∪（0，+∞），f（x）是奇函数，且当x＞0时，f（x）=x²﹣x+a，若函数g（x）=f（x）﹣x的零点恰有两个，则实数a的取值范围是（ ）

A．a＜0

B．a≤0

C．a≤1

D．a≤0或a=1

函数在定义域内的零点的个数为（    ）

A．0

B．1

C．2

D．3