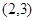若定义在R上的函数f(x)满足f(x+2)=f(x),且x∈[-1,1]时,f(x)=1-x2,函数 则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数是
则函数h(x)=f(x)-g(x)在区间[-5,5]内的零点的个数是
| A.5 | B.7 | C.8 | D.10 |
设函数f(x)=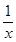 ,g(x)=-x2+bx.若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是( )
,g(x)=-x2+bx.若y=f(x)的图象与y=g(x)的图象有且仅有两个不同的公共点A(x1,y1),B(x2,y2),则下列判断正确的是( )
| A.x1+x2>0,y1+y2>0 |
| B.x1+x2>0,y1+y2<0 |
| C.x1+x2<0,y1+y2>0 |
| D.x1+x2<0,y1+y2<0 |
已知f(x﹣1)=x2,则f(x)的表达式是( )
| A.f(x)=x2+6x | B.f(x)=x2+2x+7 |
| C.f(x)=x2+2x+1 | D.f(x)=x2+2x﹣1 |
根据表格中的数据,可以断定方程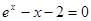 的一个根所在的区间是( )
的一个根所在的区间是( )
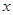 |
-1 |
0 |
1 |
2 |
3 |
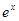 |
0.37 |
1 |
2.72 |
7.39 |
20.09 |
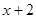 |
1 |
2 |
3 |
4 |
5 |
A.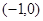 B.
B.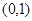 C.
C.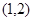 D.
D.