若函数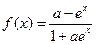 (
( 为常数)在定义域上为奇函数,则
为常数)在定义域上为奇函数,则 的值为( )
的值为( )
A.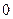 |
B.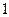 |
C.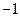 |
D.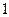 或 或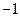 |
设 为定义在
为定义在 上的奇函数,当
上的奇函数,当 时,
时, (
( 为常数),则
为常数),则 ( )
( )
| A.3 | B.1 | C.-3 | D. |
设 为定义在
为定义在 上的奇函数,当
上的奇函数,当 时,
时, (
( 为常数),则
为常数),则 ( )
( )
| A.3 | B.1 | C.-3 | D. |
已知函数f(x) =" "  + 1 ,x<1 ,若f[f(0)] =" 4" a ,实数a等于( )
+ 1 ,x<1 ,若f[f(0)] =" 4" a ,实数a等于( )
 + a x ,x≥1
+ a x ,x≥1
A. |
B. |
C.2 | D.9 |
若函数y = ( -3a + 3)·
-3a + 3)· 是指数函数 ,则( )
是指数函数 ,则( )
| A.a = 1或a =" 2" | B.a =" 1" | C.a =" 2" | D.a>0且a≠ 1 |
已知 都是正实数, 函数
都是正实数, 函数 的图象过(0,2)点,则
的图象过(0,2)点,则 的最小值是( )
的最小值是( )
A. |
B. |
C. |
D. |
给定函数① ,②
,② ,③
,③ ,④
,④ ,其中在区间
,其中在区间
(0,1)上单调递减的函数序号是 ( )
| A.①② | B.②③ | C.③④ | D.①④ |
若lga+lgb=0(其中a≠1,b≠1),则函数f(x)=ax与g(x)=bx的图象( )
| A.关于直线y=x对称 | B.关于y轴对称 | C.关于x轴对称 | D.关于原点对称 |
Ⅰ(理)我们把形如 的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边求对数得
的函数称为幂指函数,幂指函数在求导时,可以利用对数法:在函数解析式两边求对数得 ,两边求导数,得
,两边求导数,得 ,于是
,于是 ,运用此方法可以探求得函数
,运用此方法可以探求得函数 的一个单调递增区间是
的一个单调递增区间是
A. |
B. |
C. |
D. |