河南省鹤壁高中高三第三次考试理科数学卷
在△ABC中,“cosA<cosB”是“sinA>sinB”成立的 ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分条件也不必要条件 |
来源:2011届河南省鹤壁高中高三第三次考试理科数学卷
下列有关命题的说法正确的是 ( )
A.命题“若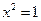 ,则 ,则 ”的否命题为:“若 ”的否命题为:“若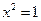 ,则 ,则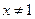 ”. ”. |
B.“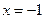 ”是“ ”是“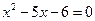 ”的必要不充分条件. ”的必要不充分条件. |
C.命题“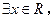 使得 使得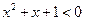 ”的否定是:“ ”的否定是:“ 均有 均有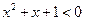 ”. ”. |
D.命题“若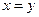 ,则 ,则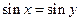 ”的逆否命题为真命题. ”的逆否命题为真命题. |
来源:2011届河南省鹤壁高中高三第三次考试理科数学卷
在下列曲线的所有切线构成的集合中,存在无数对互相垂直的切线的有( )
① ②
②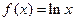 ③
③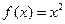 ④
④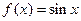
| A.1个 | B. 2个 | C.3个 | D.4个 |
来源:2011届河南省鹤壁高中高三第三次考试理科数学卷
用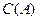 表示非空集合A中的元素个数,定义
表示非空集合A中的元素个数,定义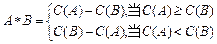 ,若
,若 ,
,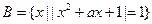 ,且
,且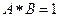 ,由
,由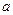 的所有可能值构成的集合是S,那么
的所有可能值构成的集合是S,那么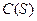 等于 ( )
等于 ( )
| A.4 | B. 3 | C.2 | D.1 |
来源:2011届河南省鹤壁高中高三第三次考试理科数学卷
在中学数学中,从特殊到一般,从具体到抽象是常见的一种思维形式如从 可抽象出
可抽象出 的性质,那么由
的性质,那么由 = (填一个具体的函数)可抽象出性质
= (填一个具体的函数)可抽象出性质
来源:2011届河南省鹤壁高中高三第三次考试理科数学卷
条件甲:“ 或
或 ”;条件乙:“
”;条件乙:“ 对x∈R恒成立”,则要使甲是乙的充要条件,命题甲的条件中须删除的一部分是_______________.
对x∈R恒成立”,则要使甲是乙的充要条件,命题甲的条件中须删除的一部分是_______________.
来源:2011届河南省鹤壁高中高三第三次考试理科数学卷
三位同学合作学习,对问题“已知不等式 对于
对于 恒成立,求
恒成立,求 的取值范围”提出了各自的解题思路.
的取值范围”提出了各自的解题思路.
甲说:“可视 为变量,
为变量, 为常量来分析”.
为常量来分析”.
乙说:“不等式两边同除以 2,再作分析”.
2,再作分析”.
丙说:“把字母 单独放在一边,再作分析”.
单独放在一边,再作分析”.
参考上述思路,或自已的其它解法,可求出实数 的取值范围是 .
的取值范围是 .
来源:2011届河南省鹤壁高中高三第三次考试理科数学卷
(本小题满分10分)已知集合 是满足下列性质的函数
是满足下列性质的函数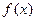 的全体:在定义域内存在
的全体:在定义域内存在 ,使得
,使得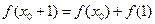 成立.
成立.
(1)试判断函数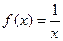 是否属于集合
是否属于集合 ?请说明理由;
?请说明理由;
(2)设函数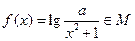 ,求实数
,求实数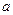 的取值范围.
的取值范围.
来源:2011届河南省鹤壁高中高三第三次考试理科数学卷
(本小题满分12分)已知函数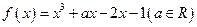
(1)若曲线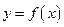 在
在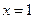 处与直线
处与直线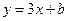 相切,求
相切,求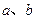 的值;
的值;
(2)若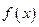 在区间
在区间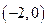 内有极值,求
内有极值,求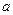 的取值范围.
的取值范围.
来源:2011届河南省鹤壁高中高三第三次考试理科数学卷
(本小题满分12分)已知△ABC中,角A、B、C的对边分别是a、b、c,且满足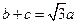 ,
,
设 ∥
∥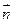 ,试求角B的大小。
,试求角B的大小。
来源:2011届河南省鹤壁高中高三第三次考试理科数学卷
已知数列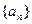 的前n项和为
的前n项和为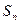 ,对一切正整数n,点
,对一切正整数n,点 都在函数
都在函数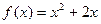 的图像上,且在点
的图像上,且在点 处的切线的斜率为
处的切线的斜率为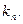
(I)求数列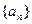 的通项公式;
的通项公式;
(II)若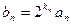 ,求数列
,求数列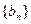 的前n项和
的前n项和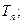
来源:2011届河南省鹤壁高中高三第三次考试理科数学卷
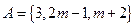 ,
,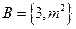 ,且
,且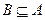 ,则
,则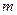 的值为( )
的值为( ) 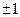
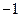
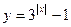 的定义域为
的定义域为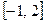 ,则其值域为 ( )
,则其值域为 ( )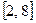
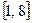
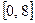

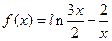 的零点一定位于区间( )
的零点一定位于区间( ) 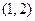
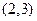
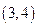
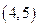
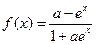 (
( 为常数)在定义域上为奇函数,则
为常数)在定义域上为奇函数,则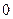
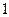
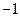
 上的函数
上的函数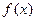 满足
满足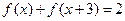 ,且
,且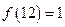 ,则
,则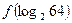 的值为
的值为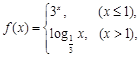 则
则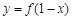 的大致图象是( )
的大致图象是( )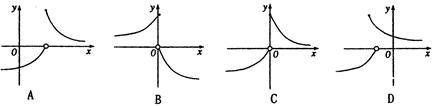
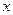 ,有
,有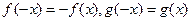 .且
.且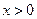 时,
时,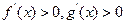 则
则 时 ( )
时 ( )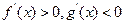
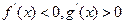
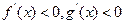
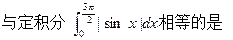 ( )
( )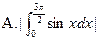
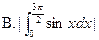
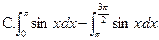
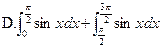

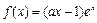 ,
,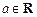
 时,求函数
时,求函数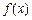 的极值;
的极值;  上是单调增函数,求实数
上是单调增函数,求实数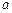 的取值范围.
的取值范围.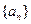 和
和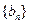 中,
中,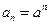 ,
,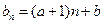 ,
,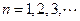 ,其中
,其中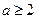 且
且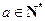 ,
,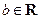 .
.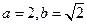 时,数列
时,数列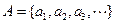 ,
,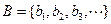 ,试问在区间
,试问在区间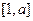 上是否存在实数
上是否存在实数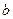 使得
使得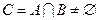 .若存在,求出
.若存在,求出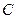 ;若不存在,试说明理由.
;若不存在,试说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号