高中数学随机思想的发展填空题

某毕业生参加人才招聘会，分别向甲、乙两个公司投递了个人简历，假定该毕业生得到甲公司面试的概率为，得到乙公司面试的概率为，且两个公司是否让其面试是相互独立的。记X为该毕业生得到面试得公司个数。若，则随机变量X的数学期望        

若随机变量的分布表如表所示，则      ▲    ．

某毕业生参加人才招聘会，分别向甲、乙、丙三个公司投递了个人简历．假定该毕业生得到甲公司面试的概率为，得到乙、丙两公司面试的概率均为p，且三个公司是否让其面试是相互独立的．记X为该毕业生得到面试的公司个数．若P(X＝0)＝，则随机变量X的数学期望E(X)＝____

现有大小形状完全相同的标号为i 的i 个球（i = 1,2,3），现从中随机取出2 个球，记取出的这两个球的标号数之和为，则随机变量的数学期望E =              ．

在某项测量中，测量结果服从正态分布．若在内取值的概率为0.35，则在内取值的概率为__________

一个袋中有大小、质地相同的标号为的三个小球.某人做如下游戏：每次从袋中摸一个小球，记下标号然后放回，共摸球次.若拿出球的标号是奇数,则得分,否则得分，则次所得分数之和的数学期望是         ．

甲定点投篮命中的概率为，现甲共投5个球，规定每投篮一次命中得3分，未命中得－1分，则甲在5次投篮中所得分数的数学期望为  ▲  分

  甲、乙两位同学参加跳远训练，在相同条件下各跳了6次，统计平均数，方差，则成绩较稳定的同学是      （填“甲”或“乙”）

随机变量的分布列如图：其中成等差数列，若，则的值是  

某班有50名学生，一次考试的成绩服从正态分布. 已知，估计该班数学成绩在110分以上的人数为______________.

将编号为1、2、3、4的4个小球随机投入到编号为1、2、3、4的4个盒中，要求每盒只投1球，记球与盒编号相同的个数为 则=            .

如图：用这3类不同的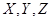元件连接成系统，每个元件是否正常工作不受其他元件的影响，当元件正常工作和元件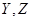中至少有
一个正常工作时，系统就正常工作。如果元件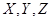
正常工作的概率分别为0.8、0.9、0.9则这个系统正常工作的概率为           .

一个袋中装有10个红球，20个白球，这些球除颜色外完全相同，一次从中摸出5个球，随机变量表示取到的红球数，服从超几何分布，则=
            （用组合数作答）

随机变量服从二项分布，则             （用数字作答）

抛掷两个骰子，取其中一个的点数为点P的横坐标，另一个的点数为点P的纵坐标，求连续抛掷这两个骰子三次，点P在圆内的次数的均值为________