某企业开展职工技能比赛,并从参赛职工中选1人参加该行业全国技能大赛.经过6轮选拔,甲、乙两人成绩突出,得分情况如茎叶图所示.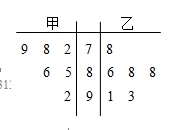
若甲乙两人的平均成绩分别是 ,
,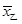 ,则下列说法正确的是( ).
,则下列说法正确的是( ).
A.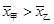 ,乙比甲成绩稳定,应该选乙参加比赛 ,乙比甲成绩稳定,应该选乙参加比赛 |
B.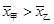 ,甲比乙成绩稳定,应该选甲参加比赛 ,甲比乙成绩稳定,应该选甲参加比赛 |
C.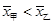 ,甲比乙成绩稳定,应该选甲参加比赛 ,甲比乙成绩稳定,应该选甲参加比赛 |
D.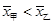 ,乙比甲成绩稳定,应该选乙参加比赛 ,乙比甲成绩稳定,应该选乙参加比赛 |
在演讲比赛决赛中,七位评委给甲、乙两位选手打分的茎叶图如图所示,但其中在 处数据丢失.按照规则,甲、乙各去掉一个最高分和一个最低分,用
处数据丢失.按照规则,甲、乙各去掉一个最高分和一个最低分,用 和
和 分别表示甲、乙两位选手获得的平均分,则( )
分别表示甲、乙两位选手获得的平均分,则( )
A. |
B. |
C. |
D. 和 和 之间的大小关系无法确定 之间的大小关系无法确定 |
某班的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是( )
| A.45 | B.50 |
| C.55 | D.60 |
容量为20的样本数据,分组后的频数如下表:
| 分组 |
[10,20) |
[20,30) |
[30,40) |
[40,50) |
[50,60) |
[60,70) |
| 频数 |
2 |
3 |
4 |
5 |
4 |
2 |
则样本数据落在区间[10,40)的频率为( )
(A)0.35 (B)0.45 (C)0.55 (D)0.65
如果一组数中每个数减去同一个非零常数,则这一组数的( )
| A.平均数不变,方差不变 | B.平均数改变,方差改变 |
| C.平均数不变,方差改变 | D.平均数改变,方差不变 |
在某项体育比赛中,七位裁判为一选手打出的分数如下:90 89 90 95 93 94 93去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为( )
A. , , |
B. , , |
C. , , |
D. , , |
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为me,众数为mo,平均值为 ,则( )
,则( )
A.me=mo= |
B.me=mo< |
C.me<mo< |
D.mo<me< |
如图,样本A和B分别取自两个不同的总体,它们的样本平均数分别为 和
和 ,样本标准差分别为sA和sB,则( )
,样本标准差分别为sA和sB,则( )
A. > > ,sA>sB ,sA>sB |
B. < < ,sA>sB ,sA>sB |
C. > > ,sA<sB ,sA<sB |
D. < < ,sA<sB ,sA<sB |
某班有50名学生,该班某次数学测验的平均分为70分,标准差为s,后来发现成绩记录有误:甲生得了80分,却误记为50分;乙生得了70分,却误记为100分.更正后得标准差为s1,则s与s1之间的大小关系为( )
| A.s<s1 | B.s>s1 |
| C.s=s1 | D.无法确定 |
在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积和的 ,且样本容量为160,则中间一组的频数为( )
,且样本容量为160,则中间一组的频数为( )
| A.32 | B.0.2 | C.40 | D.0.25 |
某中学从某次考试成绩中抽取若干名学生的分数,并绘制成如图所示的频率分布直方图,样本数据分组为 、
、 、
、 、
、 、
、 .若用分层抽样的方法从样本中抽取分数在
.若用分层抽样的方法从样本中抽取分数在 范围内的数据
范围内的数据 个,则其中分数在
个,则其中分数在 范围内的样本数据有( )
范围内的样本数据有( )
A. 个 个 |
B. 个 个 |
C. 个 个 |
D. 个 个 |
在样本的频率分布直方图中,共有11个小长方形,若中间一个长方形的面积等于其他10个小长方形面积和的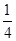 ,且样本容量为160,则中间一组的频数为( )
,且样本容量为160,则中间一组的频数为( )
| A.32 | B.0.2 | C.40 | D.0.25 |
右图是一容量为 的样本的重量的频率分布直方图,则由图可估计样本重量的中位数为( )
的样本的重量的频率分布直方图,则由图可估计样本重量的中位数为( )
A. |
B. |
C. |
D. |
样本(x1,x2,…,xn)的平均数为x,样本(y1,y2,…,ym)的平均数为y(x≠y).若样本(x1,x2,…,xn,y1,y2,…,ym)的平均数z=αx+(1-α)y,其中0<α< ,则n,m的大小关系为( )
,则n,m的大小关系为( )
| A.n<m | B.n>m | C.n=m | D.不能确定 |
通过某雷达测速点的机动车的时速频率分布直方图如图所示,则通过该测速点的机动车的时速超过60的概率是( )
| A.0.038 | B.0.38 | C.0.028 | D.0.28 |