高中数学误差估计选择题

的平均数是,方差是,则另一组的平均数和方差分别是

A．

B．

C．

D．

某产品的广告费用与销售额的统计数据如下表：

广告费用 (万元)	4	2	3	5
销售额 (万元)	49	26	39	54

根据上表可得回归方程中的为，据此模型预报广告费用为万元时销售额为(    )
A、万元                B、万元    
C、万元                D、万元

为了了解某校高三学生的视力情况，随机地抽查了该校100名高三学生，得到学生视力频率分布直方图，如右图，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频率成等差数列．设最大频率为a；视力在4．6到5．0之间的学生人数为b，则a、b的值分别为

A．0.27，78	B．0.27，83
C．2.7，78	D．2.7，83

一个容量为35的样本数据，分组后，组距与频数如下：个；个；个；个；个；个。则样本在区间上的频率为

A．20%

B．69%

C．31%

D．27%

在对某样本进行实验时，测得如下数据：则与之间的回归直线方程为（　　）

	2	1	4	3
	3	2	5	4

A、　　　B、　　　C、　　　D、

某苗圃基地为了解基地内甲、乙两块地种植的同一种树苗的长势情况，从两块地各随机抽取了10株树苗，用茎叶图表示上述两组数据，对两块地抽取树苗的高度的平均数、和中位数进行比较，下面结论正确的是

A．	B．
C．	D．

将甲、乙两名同学5次地理测验的成绩用茎叶图表示如下图，若甲、乙两人成绩的中位数分别为，则下列说法正确的是（   ）
   

A．；乙比甲成绩稳定	B．；甲比乙成绩稳定
C．；乙比甲成绩稳定	D．；甲比乙成绩稳定

一个容量为20的样本数据分组后，组距与频数如下：(10,20),2；(20,30),3；(30,40),4；(40,50),5；(50,60),4，(60,70),2.则样本在区间(－∞，50)上的频率是（   ）

A．0.20

B．0.25

C．0.50

D．0.70

为了了解某地区高三学生的身体发育情况，抽查了该地区100名年龄为17.5岁－１８岁的男生体重(kg) ,得到频率分布直方图如下：根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是（  ）

A．20

B．30

C．40

D．50

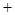
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如右图，其中甲班学生成绩的平均分是85，乙班学生成绩的中位数是83，则的值为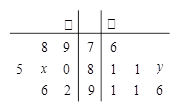

A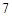．	B．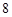
C．	D．168

如图是某次比赛上七位评委为某选手打出的分数的茎叶图，若去掉一个最高分和最低分，则所剩数据的平均数为

A．84

B．85

C．86

D．87

某工厂对一批产品进行了抽样检测.图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100),[100，102)，[102，104),[104，106],已知样本中产品净重小于100克的个数是36，则样本中净重大于或等于98克并且小于104克的产品的个数是(        ).

A．90

B．75

C． 60

D．45

为调查某校学生喜欢数学课的人数比例，采用如下调查方法：
（1）在该校中随机抽取名学生，并编号；
（2）在箱内放置两个白球和三个红球，让抽取的名学生分别从箱中随机摸出一球，记住其颜色并放回；
（3）请下列两类学生举手：（ⅰ）摸到白球且号数为偶数的学生；（ⅱ）摸到红球且不喜欢数学课的学生.
如果总共有名学生举手，那么用概率与统计的知识估计，该校学生中喜欢数学课的人数比例大约是

A．

B．

C．

D．

据《中华人民共和国道路交通安全法》规定：车辆驾驶员血液酒精浓度在20-80 mg/100ml（不含80）之间，属于酒后驾车，血液酒精浓度在80mg/100ml（含80）以上时，属醉酒驾车．据《法制晚报》报道，2012年8月15日至8月28日，全国查处酒后驾车和醉酒驾车共28800人，如图是对这28800人血液中酒精含量进行检测所得结果的频率分布直方图，则属于醉酒驾车的人数约为

A．

B．

C．

D．

如图：样本A和B分别取自两个不同的总体，他们的样本平均数分别为和，样本标准差分别为和，则（  ）

A．

B．

C．

D．