[福建]2012-2013学年福建省四地六校高二下学期第一次联考文科数学试卷
在下列四组框图中,是工序流程图的是( )
| 二楼 |
校长室 |
副校长室 |
办公室 |
||
| 一楼 |
教务处 |
政教处 |
教研室 |
团委 |
|
(3)
(4)
A、(2)(4) B、(1)(3) C、(2)(3) D、(1)(4)
甲、乙两同学投篮进球的概率分别是 和
和 ,现甲、乙各投篮一次,都不进球的概率是( )
,现甲、乙各投篮一次,都不进球的概率是( )
A. |
B. |
C. |
D. |
已知幂函数 是增函数,而
是增函数,而 是幂函数,所以
是幂函数,所以 是增函数,上面推理错误是( )
是增函数,上面推理错误是( )
| A.大前提错误导致结论错 | B.小前提错误导致结论错 |
| C.推理的方式错误导致错 | D.大前提与小前提都错误导致错 |
在对某样本进行实验时,测得如下数据:则 与
与 之间的回归直线方程为( )
之间的回归直线方程为( )
 |
2 |
1 |
4 |
3 |
 |
3 |
2 |
5 |
4 |
A、 B、
B、 C、
C、 D、
D、
下列说法中正确的是( )
A.满足方程 的 的 值为函数 值为函数 的极值点 的极值点 |
B.“ ”是“复数 ”是“复数 为纯虚数”的充要条件 为纯虚数”的充要条件 |
C.由“ ,”,推出“ ,”,推出“ ”的过程是演绎推理 ”的过程是演绎推理 |
D.“若 成等差数列,则 成等差数列,则 ”类比上述结论:若 ”类比上述结论:若 成等比数列,则 成等比数列,则 |
已知双曲线 的一个焦点与抛物线
的一个焦点与抛物线 的焦点相同,则双曲线的渐近线方程是( )
的焦点相同,则双曲线的渐近线方程是( )
A. |
B. |
C. |
D. |
已知函数 在点A处的切线垂直于
在点A处的切线垂直于 轴,则点A的横坐标是( )
轴,则点A的横坐标是( )
| A.1 | B.-1 | C. |
D. |
设抛物线 上一点P到
上一点P到 轴的距离为4,则点P到该抛物线焦点的距离是( )
轴的距离为4,则点P到该抛物线焦点的距离是( )
| A.4 | B.6 | C.8 | D.12 |
阅读如图所示程序框图,运行相应的程序( 为虚数单位),则输出的S的值为( )
为虚数单位),则输出的S的值为( )
| A.-1 | B.1 | C. |
D.0 |
椭圆两焦点为 ,
, ,P在椭圆上,若
,P在椭圆上,若 的面积最大值为12,则该椭圆的离心率是____________。
的面积最大值为12,则该椭圆的离心率是____________。
如图是杨辉三角的前五行数的结构图对应 展开式各项系数,则
展开式各项系数,则 展开式中第四项的系数应是__________。
展开式中第四项的系数应是__________。
给出下列四个判断,(1)若 ;(2)对判断“
;(2)对判断“ 都大于零”的反设是“
都大于零”的反设是“ 不都大于零”;(3)“
不都大于零”;(3)“ ,使得
,使得 ”的否定是“对
”的否定是“对 ”;(4)某产品销售量
”;(4)某产品销售量 (件)与销售价格
(件)与销售价格 (元/件)负相关,则其回归方程
(元/件)负相关,则其回归方程 ,以上判断正确的是_________。
,以上判断正确的是_________。
已知复数 ,问:当
,问:当 为何实数时?
为何实数时?
(1) 为虚数; (2)
为虚数; (2) 在复平面内对应的点在虚轴的负半轴上;
在复平面内对应的点在虚轴的负半轴上;
(3)
学校在开展学雷锋活动中,从高二甲乙两班各选3名学生参加书画比赛,其中高二甲班选出了1女2男,高二乙班选出了1男2女。
(1)若从6个同学中抽出2人作活动发言,写出所有可能的结果,并求高二甲班女同学,高二乙班男同学至少有一个被选中的概率。
(2)若从高二甲班和高二乙班各选一名现场作画,写出所有可能的结果,并求选出的2名同学性别相同的概率。
为了解目前老年人居家养老还是在敬老院养老的意向,共调查了50名老年人,其中男性明确表示去敬老院养老的有5人,女性明确表示居家养老的有10人,已知在全部50人中随机地抽取1人明确表示居家养老的概率为 。
。
(1)请根据上述数据建立一个2×2列联表;
(2)居家养老是否与性别有关?请说明理由。
参考公式:
参考数据:
 |
0.100 |
0.050 |
0.025 |
0.010 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
(1)观察下列各式:
请你根据上述特点,提炼出一个一般性命题(写出已知,求证),并用分析法加以证明。
(2)命题 ,函数
,函数 单调递减,
单调递减,
命题 上为增函数,若“
上为增函数,若“ ”为假,“
”为假,“ ”为真,求实数
”为真,求实数 的取值范围。
的取值范围。
已知椭圆C的长轴长为 ,一个焦点的坐标为(1,0).
,一个焦点的坐标为(1,0).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设直线l:y=kx与椭圆C交于A,B两点,点P为椭圆的右顶点.
(ⅰ)若直线l斜率k=1,求△ABP的面积;
(ⅱ)若直线AP,BP的斜率分别为 ,
, ,求证:
,求证: 为定值.
为定值.
 所对应的复数是( )
所对应的复数是( )



 上任取两数
上任取两数 和
和 组成有序数对
组成有序数对 ,记事件
,记事件 为“
为“ ”,则
”,则 ( )
( )



 在
在 内有极小值,则实数
内有极小值,则实数 的取值范围是( )
的取值范围是( )

 )
)
 ,满足
,满足 ,则
,则 __________。
__________。
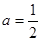 时,求函数在
时,求函数在 上的最大值和最小值;
上的最大值和最小值; 在
在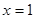 处取得极值,不等式
处取得极值,不等式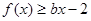 对
对 恒成立,求实数
恒成立,求实数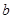 的取值范围。
的取值范围。 粤公网安备 44130202000953号
粤公网安备 44130202000953号