已知椭圆C的长轴长为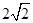 ,一个焦点的坐标为(1,0).
,一个焦点的坐标为(1,0).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设直线l:y=kx与椭圆C交于A,B两点,点P为椭圆的右顶点.
(ⅰ)若直线l斜率k=1,求△ABP的面积;
(ⅱ)若直线AP,BP的斜率分别为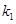 ,
,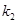 ,求证:
,求证: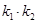 为定值.
为定值.
推荐套卷
已知椭圆C的长轴长为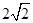 ,一个焦点的坐标为(1,0).
,一个焦点的坐标为(1,0).
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)设直线l:y=kx与椭圆C交于A,B两点,点P为椭圆的右顶点.
(ⅰ)若直线l斜率k=1,求△ABP的面积;
(ⅱ)若直线AP,BP的斜率分别为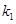 ,
,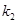 ,求证:
,求证: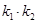 为定值.
为定值.