[湖北]2013届湖北省八市高三3月联考文科数学试卷
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如右图,其中甲班学生成绩的平均分是85,乙班学生成绩的中位数是83,则
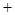
 的值为
的值为
A. |
B. |
C.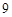 |
D.168 |
《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一,书中有这样的一道题目:把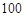 个面包分给
个面包分给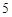 个人,使每人所得成等差数列,且使较大的三份之和的
个人,使每人所得成等差数列,且使较大的三份之和的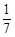 是较小的两份之和,则最小的
是较小的两份之和,则最小的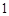 份为
份为
A. |
B.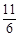 |
C. |
D. |
从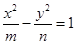 (其中
(其中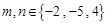 )所表示的圆锥曲线(椭圆、双曲线、抛物线)方程中任取一个,则此方程是焦点在
)所表示的圆锥曲线(椭圆、双曲线、抛物线)方程中任取一个,则此方程是焦点在 轴上的双曲线方程的概率为( )
轴上的双曲线方程的概率为( )
A.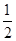 |
B.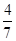 |
C. |
D. |
某高三年级有 名同学,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),若用分层抽样的方法选取
名同学,将他们的身高(单位:cm)数据绘制成频率分布直方图(如图),若用分层抽样的方法选取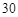 人参加一项活动,则从身高在
人参加一项活动,则从身高在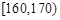 内的学生中选取的人数应为 .
内的学生中选取的人数应为 .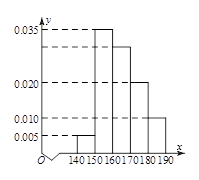
某地区恩格尔系数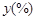 与年份
与年份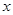 的统计数据如下表:
的统计数据如下表:
年份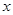 |
2004 |
2005 |
2006 |
2007 |
恩格尔系数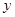 (%) (%) |
47 |
45.5 |
43.5 |
41 |
从散点图可以看出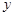 与
与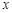 线性相关,且可得回归直线方程为
线性相关,且可得回归直线方程为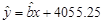 ,据此模型可预测2013年该地区的恩格尔系数(%)为 .
,据此模型可预测2013年该地区的恩格尔系数(%)为 .
下表中数阵为“森德拉姆素数筛”,其特点是每行每列都成等差数列,记第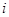 行第
行第 列的数为
列的数为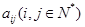 ,则:
,则: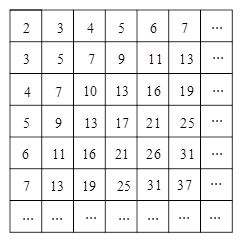
(Ⅰ)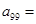 ; (Ⅱ)表中数
; (Ⅱ)表中数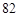 共出现 次.
共出现 次.
(本小题满分12分)已知A、B、C为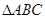 的三个内角且向量
的三个内角且向量 共线。
共线。
(Ⅰ)求角C的大小:
(Ⅱ)设角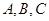 的对边分别是
的对边分别是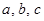 ,且满足
,且满足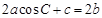 ,试判断
,试判断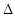
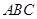 的形状.
的形状.
(本小题满分12分)在等差数列 中,
中, ,
,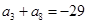 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列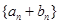 是首项为
是首项为 ,公比为
,公比为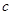 的等比数列,求
的等比数列,求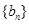 的前
的前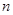 项和
项和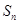 .
.
(本小题满分13分)如图所示,四棱锥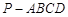 中,底面
中,底面 是边长为2的菱形,
是边长为2的菱形,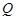 是棱
是棱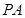 上的动点.
上的动点.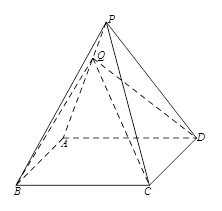
(Ⅰ)若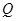 是
是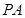 的中点,求证:
的中点,求证: //平面
//平面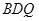 ;
;
(Ⅱ)若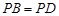 ,求证:
,求证: ;
;
(III)在(Ⅱ)的条件下,若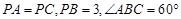 ,求四棱锥
,求四棱锥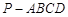 的体积.
的体积.
(本大题满分14分)
已知△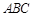 的两个顶点
的两个顶点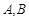 的坐标分别是
的坐标分别是 ,
,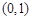 ,且
,且 所在直线的斜率之积等于
所在直线的斜率之积等于 .
.
(Ⅰ)求顶点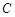 的轨迹
的轨迹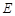 的方程,并判断轨迹
的方程,并判断轨迹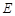 为何种圆锥曲线;
为何种圆锥曲线;
(Ⅱ)当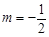 时,过点
时,过点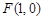 的直线
的直线 交曲线
交曲线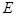 于
于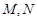 两点,设点
两点,设点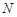 关于
关于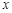 轴的对称点为
轴的对称点为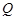 (
( 不重合).求证直线
不重合).求证直线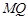 与
与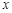 轴的交点为定点,并求出该定点的坐标.
轴的交点为定点,并求出该定点的坐标.
 ,
,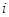 是虚数单位,且
是虚数单位,且 ,则
,则 的值为
的值为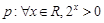 ,那么命题
,那么命题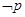 为
为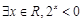
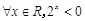
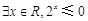
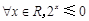
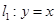 ,若直线
,若直线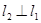 ,则直线
,则直线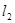 的倾斜角为
的倾斜角为
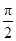
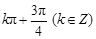
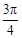
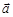 与
与 的夹角为
的夹角为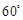 ,
, ,
,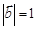 ,则
,则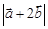
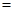


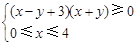 表示的平面区域是
表示的平面区域是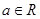 ,函数
,函数 的导函数是
的导函数是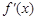 ,且
,且 的值为
的值为
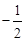

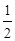
 ,,则函数
,,则函数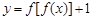 的零点个数是
的零点个数是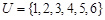 ,
,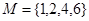 ,则
,则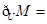 .
.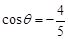 ,且
,且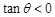 ,则
,则 .
.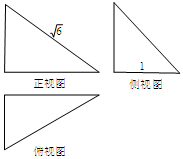
 ,若执行如下左图所示的程序框图,则输出的
,若执行如下左图所示的程序框图,则输出的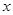 不小于 47的概率为 .
不小于 47的概率为 . 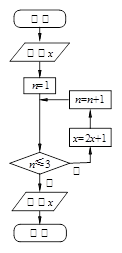
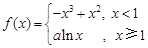 ,其中
,其中
 在
在 上的单调区间;
上的单调区间;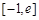 (
(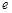 为自然对数的底数)上的最大值;
为自然对数的底数)上的最大值;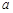 ,曲线
,曲线 上是否存在两点
上是否存在两点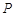 、
、 ,使得
,使得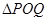 是以原点
是以原点 为直角顶点的直角三角形,且此三角形斜边中点在
为直角顶点的直角三角形,且此三角形斜边中点在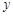 轴上?
轴上? 粤公网安备 44130202000953号
粤公网安备 44130202000953号