高中数学随机事件试题

种植某种树苗，成活率为，现采用随机模拟的方法估计该树苗种植棵恰好
棵成活的概率，先由计算机产生到之间取整数值的随机数，指定至的数字代表成
活，代表不成活，再以每个随机数为一组代表次种植的结果。经随机模拟产生如下
组随机数：
                              
据此估计，该树苗种植棵恰好棵成活的概率为

A．

B．

C．

D．

同时抛掷两枚骰子，则至少有一个5点或6点的概率是(   )

A．

B．

C．

D．

已知圆，点是圆内的任意一点，直线.
（1）求点在第一象限的概率；
（2）若，求直线与圆相交的概率.

甲，乙两队进行排球决赛，现在的情形是甲队只要再赢一局就获冠军，乙队需要再赢两局才能得冠军，若两队胜每局的概率相同，则甲队获得冠军的概率为（    ）

A．

B．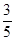

C．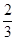

D．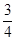

在15个村庄中有7个村庄交通不便，现从中任意选10个村庄，用ξ表示这10个村庄中交通不便的村庄数，下列概率中等于的是(　　)

A．P(ξ＝2)	B．P(ξ≤2)
C．P(ξ＝4)	D．P(ξ≤4)

一条生产线上生产的产品按质量情况分为三类：A类、B类、C类．检验员定时从该生产线上任取2件产品进行一次抽检，若发现其中含有C类产品或2件都是B类产品，就需要调整设备，否则不需要调整．已知该生产线上生产的每件产品为A类品，B类品和C类品的概率分别为0.9,0.05和0.05，且各件产品的质量情况互不影响．
(1)求在一次抽检后，设备不需要调整的概率；
(2)若检验员一天抽检3次，以ξ表示一天中需要调整设备的次数，求ξ的分布列．

在不等式组所表示的平面区域内的所有格点(横、纵坐标均为整数的点称为格点)中任取3个点，则该3点恰能作为一个三角形的3个顶点的概率为________．

在区间[﹣2，4]上随机地取一个数x，则满足|x|≤ 3的概率为     

甲、乙两人一起去游玩，他们约定各自独立地从1到6号景点中任选4个进行游览，每个景点参观1小时，则最后1小时他们在同一个景点的概率是(　　)

A．

B．

C．

D．

现有10个数，它们能构成一个以1为首项，－3为公比的等比数列，若从这10个数中随机抽取一个数，则它小于8的概率是______．

如图，长方体ABCD—A₁B₁C₁D₁，有一动点在此长方体内随机运动，则此动点在三棱锥A—A₁BD内的概率为   ．

一个篮球运动员投篮一次得分的概率为，得分的概率为，得分的概率为（投篮一次得分只能分、分、分或分），其中，已知他投篮一次得分的数学期望为，则的最大值为（     ）

A．

B．

C．

D．

某城市要建成宜商、宜居的国际化现代新城，该城市的东城区、西城区分别引进8甲厂家，现对两个区域的16个厂家进行评估，综合得分情况如茎叶图所示.

（1）根据茎叶图判断哪个区域厂家的平均分较高；
（2）规定85分以上（含85分）为优秀厂家，若从该两个区域各选一个优秀厂家，求得分差距不超过5分的概率.

在30瓶饮料中，有3瓶已过了保质期，从这30瓶饮料中任取2瓶，则至少取到1瓶已过保质期的概率为________(结果用最简分数表示)．

掷一枚均匀的硬币两次，事件M：一次正面朝上，一次反面朝上，事件N：至少一次正面朝上，则下列结果正确的是(　　)

A．P(M)＝，P(N)＝	B．P(M)＝，P(N)＝
C．P(M)＝，P(N)＝	D．P(M)＝，P(N)＝