变量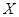 与
与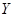 相对应的一组数据为
相对应的一组数据为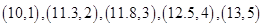 ,变量
,变量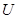 与
与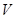 相对应的一组数据为
相对应的一组数据为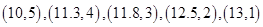 .
.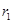 表示变量
表示变量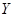 与
与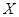 之间的线性相关系数,
之间的线性相关系数,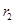 表示变量
表示变量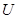 与
与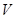 之间的线性相关系数,则( )
之间的线性相关系数,则( )
A.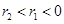 |
B.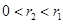 |
C.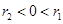 |
D. |
容量为100的样本数据,按从小到大的顺序分为8组,如下表:
第三组的频数和频率分别是 ( )
A. 和0.14 和0.14 |
B.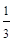 和 和 |
C.14和0.14 | D.0.14和14 |
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了下表:
| |
喜爱打篮球 |
不喜爱打篮球 |
合计 |
| 男生 |
20 |
5 |
25 |
| 女生 |
10 |
15 |
25 |
| 合计 |
30 |
20 |
50 |
则根据表中的数据,计算随机变量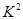 的值,并参考有关公式,你认为性别与是否喜爱打篮球之间有关系的把握有
的值,并参考有关公式,你认为性别与是否喜爱打篮球之间有关系的把握有
A.0 B.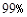 C .99.5% D.
C .99.5% D.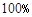
为研究变量 的线性相关性,甲、乙二人分别作了研究,利回线性回归方法
的线性相关性,甲、乙二人分别作了研究,利回线性回归方法
得到回归直线方程 ,两人计算知
,两人计算知 相同,
相同, 也相同,下列正确的是( )
也相同,下列正确的是( )
A. 重合 重合 |
B. 一定平行 一定平行 |
C. |
D.无法判断 是否相交 是否相交 |
在一次实验中,采集到如下一组数据:
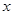 |
-2.0 |
-1.0 |
0 |
1.00 |
2.00 |
3.00 |
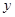 |
0.24 |
0.51 |
1 |
2.02 |
3.98 |
8.02 |
则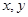 的函数关系与下列( )类函数最接近(其中
的函数关系与下列( )类函数最接近(其中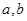 为待定系数)
为待定系数)
A.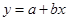 B .
B .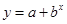 C.
C.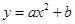 D.
D.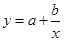
某农贸市场出售西红柿,当价格上涨时,供给量相应增加,而需求量相应减少,具体调查结果如下表:
表1 市场供给量 表2 市场需求量
| 单价 (元/kg) |
2 |
2.4 |
2.8 |
3.2 |
3.6 |
4 |
单价 (元/kg) |
4 |
3.4 |
2.9 |
2.6 |
2.3 |
2 |
| 供给量 (1000kg) |
50 |
60 |
70 |
75 |
80 |
90 |
需求量 (1000kg) |
50 |
60 |
65 |
70 |
75 |
80 |
根据以上提供的信息,市场供需平衡点(即供给量和需求量相等时的单价)应在区间( )
A.(2.3,2.6)内 B.(2.4,2.6)内 C.(2.6,2.8)内 D.(2.8,2.9)内
如图,样本 和 分别取自两个不同的总体,它们的样本平均数分别为 ,样本标准差分别为 和 ,则( )
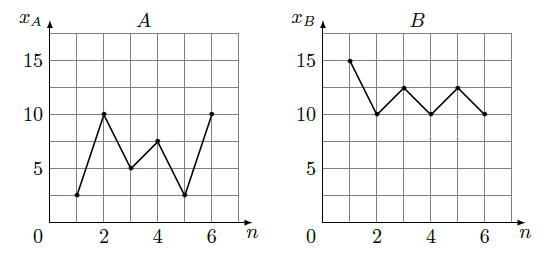
| A. | , |
| B. | , |
| C. | , |
| D. | , |
某医疗研究所为了检验新开发的流感疫苗对甲型H1N1流感的预防作用,把1000名注射了疫苗的人与另外1000名未注射疫苗的人的半年的感冒记录作比较,提出假设H0:“这种疫苗不能起到预防甲型H1N1流感的作用”,经计算得到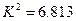 ,且
,且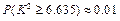 ,则下列说法正确的是( )
,则下列说法正确的是( )
| A.这种疫苗能起到预防甲型H1N1流感的有效率为1% |
| B.若某人未使用该疫苗,则他在半年中有99%的可能性得甲型H1N1 |
| C.有1%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用” |
| D.有99%的把握认为“这种疫苗能起到预防甲型H1N1流感的作用. |
假设关于某设 备的使用年限
备的使用年限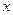 (年)和所支出的维修费用
(年)和所支出的维修费用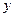 (万元)有如下统计资料:
(万元)有如下统计资料:
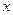 (年) (年) |
2 |
3 |
4 |
5 |
6 |
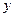 (万元) (万元) |
2.2 |
3.8 |
5.5 |
6.5 |
7.0 |
若由资料知,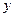 对
对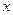 呈线性相关关系,且有如下参考数据:
呈线性相关关系,且有如下参考数据: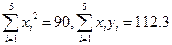 ,则回归直线方程为
,则回归直线方程为
A. |
B.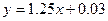 |
C.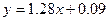 |
D.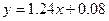 |
下列四个命题正确的是 ( )
①线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越小;
②残差平方和越小的模型,拟合的效果越好;
③用相关指数R2来刻画回归效果,R2越小,说明模型的拟合效果越好。
④随机误差e是衡量预报精确度的一个量,它满足E(e)=0
| A.①③ | B.②④ | C.①④ | D.②③ |