设命题p:{x|x2-4ax+3a2<0}(a>0), .
.
(1)如果a=1,且p∧q为真时,求实数x的取值范围;
(2)若¬p是¬q的充分不必要条件时,求实数a的取值范围.
已知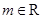 ,“函数
,“函数 有零点”是“函数
有零点”是“函数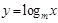 在
在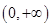 上为减函数”的( )
上为减函数”的( )
| A.充分不必要条件 |
| B.必要不充分条件 |
| C.充要条件 |
| D.既不充分也不必要条件 |
下列说法错误的是( )
| A.若p:∃x∈R,x2-x+1=0,则¬p:∀x∈R,x2-x+1≠0 |
B.“sinθ=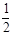 ”是“θ=30°”的充分不必要条件 ”是“θ=30°”的充分不必要条件 |
| C.命题“若a=0,则ab=0”的否命题是“若a≠0,则ab≠0” |
| D.已知p:∃x∈R,cosx=1,q:∀x∈R,x2-x+1>0,则“p∧(¬q)”为假命题 |
设函数 的定义域为R,则
的定义域为R,则 是“函数
是“函数 为奇函数”的( )
为奇函数”的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
已知命题 “存在
“存在 ”,命题
”,命题 :“曲线
:“曲线 表示焦点在
表示焦点在 轴上的椭圆”,命题
轴上的椭圆”,命题 “曲线
“曲线 表示双曲线”.
表示双曲线”.
(1)若“ 且
且 ”是真命题,求
”是真命题,求 的取值范围;
的取值范围;
(2)若 是
是 的必要不充分条件,求
的必要不充分条件,求 的取值范围.
的取值范围.
给出如下四个命题:
①若“ 且
且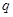 ”为假命题,则
”为假命题,则 、
、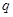 均为假命题;
均为假命题;
②命题“若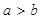 ,则
,则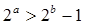 ”的否命题为“若
”的否命题为“若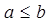 ,则
,则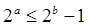 ”;
”;
③“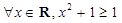 ”的否定是“
”的否定是“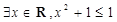 ”;
”;
④在△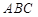 中,“
中,“ ”是“
”是“ ”的充要条件.
”的充要条件.
其中不正确的命题的个数是( )
| A.4 | B.3 | C.2 | D.1 |
下列叙述中正确的是( )
A.若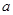 , , , ,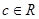 ,则“ ,则“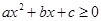 ”的充分条件是“ ”的充分条件是“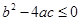 ” ” |
B.若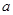 , , , ,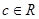 ,则“ ,则“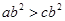 ”的充要条件是“ ”的充要条件是“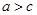 ” ” |
C.命题“对任意 ,有 ,有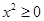 ”的否定是“存在 ”的否定是“存在 ,有 ,有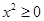 ” ” |
D. 是一条直线, 是一条直线,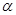 , ,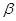 是两个不同的平面,若 是两个不同的平面,若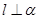 , , ,则 ,则 |