如图,ABEDFC为多面体,平面ABED与平面ACFD垂直,点O在线段AD上,OA=1,OD=2,△OAB,△OAC,△ODE,△ODF都是正三角形.
(1)证明直线BC∥EF;
(2)求棱锥F OBED的体积.
OBED的体积.
如图,在侧棱垂直底面的四棱柱ABCD A1B1C1D1中,AD∥BC,AD⊥AB,AB=
A1B1C1D1中,AD∥BC,AD⊥AB,AB= ,AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
,AD=2,BC=4,AA1=2,E是DD1的中点,F是平面B1C1E与直线AA1的交点.
(1)证明:①EF∥A1D1;②BA1⊥平面B1C1EF.
(2)求BC1与平面B1C1EF所成的角的正弦值.
如图,两条相交线段 、
、 的四个端点都在抛物线
的四个端点都在抛物线 上,其中,直线
上,其中,直线 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 .
.
(1)若 ,
, ,求
,求 的值;
的值;
(2)探究:是否存在常数 ,当
,当 变化时,恒有
变化时,恒有 ?
?
设函数 ,
, ,
, .
.
(1)若 ,求
,求 的单调递增区间;
的单调递增区间;
(2)若曲线 与
与 轴相切于异于原点的一点,且
轴相切于异于原点的一点,且 的极小值为
的极小值为 ,求
,求 的值.
的值.
已知函数 .
.
(1)若 ,求
,求 的取值范围;
的取值范围;
(2)设△ 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知 为锐角,
为锐角, ,
, ,
, ,求
,求 的值.
的值.
已知双曲线C: 的离心率为2,
的离心率为2, 为期左右顶点,点P为双曲线C在第一象限的任意一点,点O为坐标原点,若
为期左右顶点,点P为双曲线C在第一象限的任意一点,点O为坐标原点,若 的斜率为
的斜率为 ,则
,则 的取值范围为( )
的取值范围为( )
A. |
B. |
C. |
D. |
设函数 ,
, ,
, ,
,
(1)若曲线 与
与 轴相切于异于原点的一点,且函数
轴相切于异于原点的一点,且函数 的极小值为
的极小值为 ,求
,求 的值;
的值;
(2)若 ,且
,且 ,
,
①求证: ; ②求证:
; ②求证: 在
在 上存在极值点.
上存在极值点.
如图,两条相交线段 、
、 的四个端点都在椭圆
的四个端点都在椭圆 上,其中,直线
上,其中,直线 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 .
.
(1)若 ,
, ,求
,求 的值;
的值;
(2)探究:是否存在常数 ,当
,当 变化时,恒有
变化时,恒有 ?
?
如图,四棱锥 的底面ABCD是平行四边形,
的底面ABCD是平行四边形, ,
, ,
, 面
面 ,设
,设 为
为 中点,点
中点,点 在线段
在线段 上且
上且 .
.
(1)求证: 平面
平面 ;
;
(2)设二面角 的大小为
的大小为 ,若
,若 ,求
,求 的长.
的长.
设数列 的前n项和为
的前n项和为 ,
, ,且
,且 成等比数列,当
成等比数列,当 时,
时, .
.
(1)求证:当 时,
时, 成等差数列;
成等差数列;
(2)求 的前n项和
的前n项和 .
.
已知函数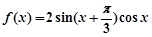 .
.
(1)若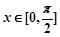 ,求
,求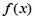 的取值范围;
的取值范围;
(2)设△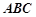 的内角A、B、C所对的边分别为a、b、c,已知
的内角A、B、C所对的边分别为a、b、c,已知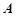 为锐角,
为锐角,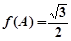 ,
,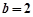 ,
,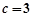 ,求
,求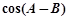 的值.
的值.
对非零实数 ,定义运算
,定义运算 满足:(1)
满足:(1) ; (2)
; (2)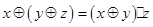 .若
.若 ,则下列判断正确的是( )
,则下列判断正确的是( )
A.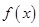 是增函数又是奇函数 是增函数又是奇函数 |
B.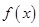 是减函数又是奇函数 是减函数又是奇函数 |
C.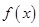 是增函数又是偶函数 是增函数又是偶函数 |
D.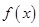 是减函数又是偶函数 是减函数又是偶函数 |
在直角 中,
中, ,P为AB边上的点
,P为AB边上的点 ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( )
A. |
B. |
C. |
D. |
已知函数 ,
,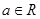 ,
, .
.
(1)若当 时,恒有
时,恒有 ,求
,求 的最大值;
的最大值;
(2)若当 时,恒有
时,恒有 ,求
,求 的取值范围.
的取值范围.