(本小题满分12分)
设数列 满足
满足 ,且对任意
,且对任意 ,函数
,函数 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,记数列
,记数列 的前项和为
的前项和为 ,求证:
,求证: .
.
在锐角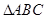 中,内角
中,内角 、
、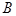 、
、 的对边分别为
的对边分别为 、
、 、
、 ,已知
,已知 ,
, ,则
,则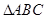 的面积取最大值时有
的面积取最大值时有 .
.
已知定义域为 的函数
的函数 ,若对任意的
,若对任意的 ,有
,有 ,则称函数
,则称函数 为“定义域上的
为“定义域上的 函数”,以下五个函数:①
函数”,以下五个函数:① ;②
;② ; ③
; ③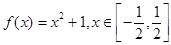 ;④
;④ ;⑤
;⑤ ,其中是“定义上的
,其中是“定义上的 函数”的有
函数”的有
| A.2个 | B.3个 | C.4个 | D.5个 |
设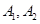 分别为双曲线
分别为双曲线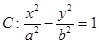
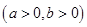 的左右顶点,若双曲线上存在点
的左右顶点,若双曲线上存在点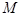 使得两直线斜率
使得两直线斜率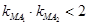 ,则双曲线
,则双曲线 的离心率的取值范围为
的离心率的取值范围为
A.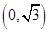 |
B.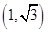 |
C.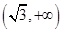 |
D.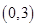 |
已知一个几何体的三图如图所示,山该几何体的体积为
A. |
B. |
C. |
D. |
已知向量 ,则函数
,则函数 的最小正周期与最大值分别为
的最小正周期与最大值分别为
A. |
B. |
C. |
D. |
运行如下程序框图:
若输出的的 值为12,则判断框中
值为12,则判断框中 的值可以是
的值可以是
| A.2 | B.3 | C.4 | D.5 |
已知抛物线 ,则
,则
A.它的焦点坐标为 |
B.它的焦点坐标为 |
C.它的准线方程是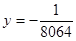 |
D.它的准线方程是 |
设二次函数 (
( ,
, ),
),
满足条件:①当 时,
时, ,且
,且 ;
;
②当 时,
时, ;
;
③f(x)在R上的最小值为0.
求最大值m( ),使得存在
),使得存在 ,只要
,只要 ,就有
,就有 .
.
设A、B是两个非空集合,定义A与B的差集 .
.
(1)试举出两个数集,使它们的差集为单元素集合;
(2)差集 与
与 是否一定相等?请说明理由;
是否一定相等?请说明理由;
(3)已知 ,
, ,求
,求 及
及 ,由此你可以得到什么更一般的结论?(不必证明)
,由此你可以得到什么更一般的结论?(不必证明)