在底面是矩形的四棱锥PABCD中,PA⊥平面ABCD,PA=AB=2,BC=4,E是PD的中点.
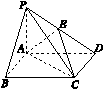
(1)求证:平面PDC⊥平面PAD;
(2)求二面角EACD的余弦值;
(3)求直线CD与平面AEC所成角的正弦值.
以A表示值域为R的函数组成的集合,B表示具有如下性质的函数 组成的集合:对于函数
组成的集合:对于函数 ,存在一个正数M,使得函数
,存在一个正数M,使得函数 的值域包含于区间
的值域包含于区间 .例如,当
.例如,当 .现有如下命题:
.现有如下命题:
①设函数 的定义域为D,则“
的定义域为D,则“ ”的充要条件是“
”的充要条件是“ ”;
”;
②函数 的充要条件是
的充要条件是 有最大值和最小值;
有最大值和最小值;
③若函数 ,
, 的定义域相同,且
的定义域相同,且
④若函数 有最大值,则
有最大值,则 .
.
其中的真命题为( )
| A.①③ | B.②③ | C.①②④ | D.①③④ |
已知向量a,b满足|a|=2|b|≠0,且关于x的函数f(x)=2x3-3| a |x2+6 a •b x+5在实数集R
上有极值,则向量a,b的夹角的取值范围是( )
A.( ,π) ,π) |
B.( ,π] ,π] |
C.[ ,π] ,π] |
D.(0, ) ) |
如图所示,在长方体 中,
中, ,
, ,M是棱
,M是棱 的中点.
的中点.
(1)求异面直线 和
和 所成的角的正切值;
所成的角的正切值;
(2)证明:平面 平面
平面 .
.
集合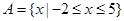 ,
,  .
.
(1)若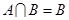 ,求实数m的取值范围;
,求实数m的取值范围;
(2)当 时,求A的非空真子集的个数.
时,求A的非空真子集的个数.
下列命题中:
①偶函数的图象一定与y轴相交;
②奇函数的图象一定过原点;
③若奇函数 ,则实数
,则实数 ;
;
④图象过原点的奇函数必是单调函数;
⑤函数 的零点个数为2;
的零点个数为2;
⑥互为反函数的图象关于直线 对称.
对称.
上述命题中所有正确的命题序号是 .