初中数学二次函数在给定区间上的最值试题

二次函数y=ax²+bx+c图象的一部分如图6所示，其对称轴为直线x=1，若其与x轴一交点为A（3，0），则由图象可知方程ax²+bx+c=0的根是　 　　　　．

如图11-1，有一座抛物线型拱桥，涨潮时桥内水面宽AB为8米，落潮时水位下降5米，桥内水面宽CD为12米．
（1）建立适当的平面直角坐标系，并求此抛物线的解析式；
（2）如图11-2，某种货船在水面上的部分的横截面是梯形EFGH，且HE=FG，EF= 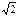HE，∠GHE=45°．试问落潮时，能顺利通过拱桥的这种货船在水面上的部分最大高度是多少？

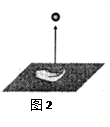
如图2，从地面竖立向上抛出一个小球，小球的高度h（单位：m）与 小球运动时间t（单位：s）之间的关系式为h=30t-5t²，那么小球从抛出至回落到地面所需要的时间是（   ）．

A．6s

B．4s

C．3s

D．2s

在一幅长为80cm，宽为50cm的矩形风景画的四周镶一条相同宽度的金色纸边，制成一幅矩形挂图，如图1所示，如果要使整个挂图的面积是5400cm²，设金色纸边的宽为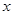cm，那么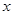满足的方程是  （   ）．

A．	B．
C．	D．

把抛物线向右平移1个单位，所得抛物线的函数表达式为   （     ）．

A．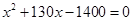

B．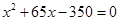

C．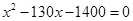

D．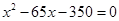

如图，抛物线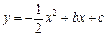与x轴交于A、B两点（A点在B点左侧），与y轴交于点C，对称轴为直线，OA = 2，OD平分∠BOC交抛物线于点D（点D在第一象限）．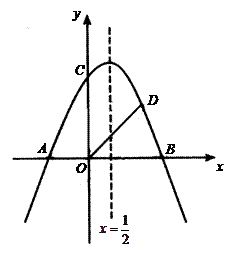

（１）求抛物线的解析式和点D的坐标；
（２）在抛物线的对称轴上，是否存在一点P，使得△BPD的周长最小？若存在，请求出点P的坐标；若不存在，请说明理由．
（３）点M是抛物线上的动点，在x轴上是否存在点N，使A、D、M、N四个点为顶点的四边形是平行四边形？如果存在，求出所有满足条件的M点坐标；如果不存在，请说明理由．

（本小题满分8分）
如图，已知抛物线C₁与坐标轴的交点依次是A（－4，0），B（－2，0），E（0，8）。
（1）求抛物线C₁关于原点对称的抛物线C₂的解析式；
（2）设抛物线C₁的顶点为M，抛物线C₂与x轴分别交于C、D两点（点C在点 D的左侧），顶点为N，四边形MDNA的面积为S。若点A、点D同时以每秒1个单位的速度沿水平方向分别向右、向左运动；与此同时，点M、点N同时以每秒2个单位的速度沿竖直方向分别向下、向上运动，直到点A与点D重合为止。求出四边形MDNA的面积S与运动时间t之间的关系式，并写出自变量t的取值范围；
（3）当t为何值时，四边形MDNA的面积S有最大值，并求出此最大值；
（4）在运动过程中，四边形MDNA能否形成矩形？若能，求出此时t的值；若不能，请说明理由．

（本小题满分7分）
某公园有一个抛物线形状的观景拱桥ABC，其横截面如图所示，在图中建立的直角坐标系中，抛物线的解析式为且过顶点C（0，5）（长度单位：m）
（1）直接写出c的值；
（2）现因搞庆典活动，计划沿拱桥的台阶表面铺设一条宽度为1.5 m的地毯，地毯的价格为20元 / ,求购买地毯需多少元？
（3）在拱桥加固维修时，搭建的“脚手架”为矩形EFGH（H、G分别在抛物线的左右侧上），并铺设斜面EG.已知矩形EFGH的周长为27.5 m，求斜面EG的坡度．

（本小题满分5分）
已知二次函数中，函数与自变量的部分对应值如下表：

	…							…
	…							…

 
（1）求该二次函数的关系式；
（2）当为何值时，有最小值，最小值是多少？
（3）若≥2，且，两点都在该函数的图象上，试比较与的大小．

（本小题满分5分）  
已知二次函数y=ax²＋bx－3的图象经过点A（2，－3），B（－1，0）．
（1）求二次函数的解析式；
（2）要使该二次函数的图象与x轴只有一个交点，应把图象沿y轴向上平移多少个单位？

将抛物线 向右平移2个单位后，所得抛物线的顶点坐标是_________；

二次函数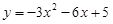的图像的顶点坐标是                

A．（-1，8）

B．（1，8）

C．（-1，2）

D．（1，-4）

如图1，已知矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3；抛物线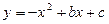经过坐标原点O和x轴上另一点E（4,0）
（1）当x取何值时，该抛物线的最大值是多少？
（2）将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从点A出发向B匀速移动.设它们运动的时间为t秒（0≤t≤3），直线AB与该抛物线的交点为N（如图2所示）.
① 当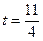时，判断点P是否在直线ME上，并说明理由；
② 以P、N、C、D为顶点的多边形面积是否可能为5，若有可能，求出此时N点的坐标；若无可能，请说明理由．

抛物线图像向右平移2个单位再向下平移3个单位，所得图像的解析式为，则b、c的值为

A．b=2， c=2

B． b=2，c=0

C．b= -2，c=-1

D． b= -3， c=2

抛物线图像如图所示，则一次函数与反比例函数在同一坐标系内的图像大致为