有一个转盘被分成白色和黑色两个区域,白色区域的圆心角是144°,如图,让转盘自由转动两次.指针一次落在黑色区域,另一次落在白色区域的概率是 .

小明任意掷一枚均匀的骰子5次,数字3正面朝上共出现了4次,则小明任意抛掷该骰子一次,数字3正面朝上的概率是( )
A. |
B. |
C. |
D.不能确定 |
把一副扑克牌中的三张黑桃牌(它们正面的数字分别为3,4,5)洗匀后正面朝下放在桌面上.小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽取一张牌,记下牌面数字后放回,洗匀后正面朝下,再由小李随机抽取一张牌,记下牌面数字.当两张牌的牌面数字相同时,小王赢;当两张牌的牌面数字不同时,小李赢.现请你利用画树状图或列表的方法分析游戏规则对双方是否公平,并说明理由.
在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同,小明通过多次摸球试验后发现从中摸到红色球、黑色球的频率稳定在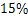 和
和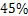 ,则口袋中白色球的个数可能是( )
,则口袋中白色球的个数可能是( )
| A.24 | B.18 | C.16 | D.6 |
下列说法正确的是( )
| A.“明天降雨的概率是80%”表示明天有80%的时间都在降雨 |
B.“抛一枚硬币正面朝上的概率为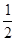 ”表示每抛2次就有一次正面朝上 ”表示每抛2次就有一次正面朝上 |
| C.“彩票中奖的概率为1%”表示买100张彩票肯定会中奖 |
D.“抛一枚正方体骰子,朝上的点数为2的概率为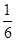 ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在 ”表示随着抛掷次数的增加,“抛出朝上的点数为2”这一事件发生的频率稳定在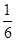 附近. 附近. |
在3×3的方格纸中,点 、
、 、
、 、
、 、
、 、
、 分别位于如图所示的小正方形的顶点上.
分别位于如图所示的小正方形的顶点上.
(1)从 、
、 、
、 、
、 四个点中任意取一点,以所取的这一点及点
四个点中任意取一点,以所取的这一点及点 、
、 为顶点画三角形,则所画三角形是等腰三角形的概率是 .
为顶点画三角形,则所画三角形是等腰三角形的概率是 .
(2)从 、
、 、
、 、
、 四个点中先后任意取两个不同的点,以所取的这两点及点
四个点中先后任意取两个不同的点,以所取的这两点及点 、
、 为顶点画四边形,求所画四边形是 平行四边形的概率(用树状图或列表法求解)
为顶点画四边形,求所画四边形是 平行四边形的概率(用树状图或列表法求解)

如图,有三条绳子穿过一片木板,姊妹两人分别站在木板的左、右两边,各选该边的一段绳子。若每边每段绳子被选中的机会相等,则两人选到同一条绳子的概率为( )

A. |
B. |
C. |
D. |
甲、乙两同学只有一张乒乓球比赛的门票,谁都想去,最后商定通过转盘游戏决定.游戏规则是:转动下面平均分成三个扇形且标有不同颜色的转盘,转盘连续转动两次,若指针前后所指颜色相同,则甲去;否则乙去.(如果指针恰好停在分割线上,那么重转一次,直到指针指向一种颜色为止)
(1)转盘连续转动两次,指针所指颜色共有几种情况?通过画树状图或列表法加以说明;
(2)你认为这个游戏公平吗?请说明理由.
两个不透明的袋子,一个装有两个球(1 个白球,一个红球),另一个装有3个球(1个白球,1个红球,1个绿球),小球除颜色不同外,其余完全相同.现从两个袋子中各随机摸出1个小球,两球颜色恰好相同的概率是 .
以下说法合理的是( )
| A.小明在10次抛图钉的试验中发现3次钉尖朝上,由此他说钉尖朝上的概率是30% |
B.抛掷一枚普通的正六面体骰子,出现6的概率是 的意思是每6次就有1次掷得6 的意思是每6次就有1次掷得6 |
| C.某彩票的中奖机会是2%,那么如果买100张彩票一定会有2张中奖。 |
| D.在一次课堂进行的试验中,甲、乙两组同学估计硬币落地后,正面朝上的概率分别为0.48和0.51。 |
在一个不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,现从中任意摸出一个是白球的概率为 .
.
(1)试求袋中蓝球的个数.
(2)第一次任意摸一个球(不放回),第二次再摸一个球,请用画树状图或列表格法,求两次摸到都是白球的概率.