初中数学相似多边形的性质试题

如图所示，给出下列条件：①；②；③；④⑤其中单独能够判定的个数为（  ）

A．2

B．3

C．4

D．5

如图，每个小正方形边长均为1，则下列图中的三角形（阴影部分）与左图中相似的是（   ）

如图，已知D、E分别是△ABC的的AB、AC边上的一点，DE∥BC，且AD: AB=1:2，则△ADE与四边形DBCE的面积之比为（   ）

A．1:4       B．1:3     C．1:2   D．2:3

两个相似三角形的最长边分别是35和14，它们的周长差是60，则大三角形的周长为（  ）

A．80

B．36

C．40

D．100

如图，△ABC中，A，B两个顶点在x轴的上方，点C的坐标是（-1，0）．以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B′C，并把△ABC的边长放大到原来的2倍．设点B的对应点B′的横坐标是a，则点B的横坐标是       ．

如图，DE是ΔABC的中位线，则ΔADE与ΔABC的面积之比是       ．

如图，平行四边形ABCD中，点E是边AD的中点，EC交对角线BD于点F，则EF∶FC等于（   ）

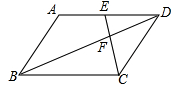
A．3∶2

B．3∶1

C．1∶1

D．1∶2

如图，小东用长为3．2m的竹竿做测量工具测量学校旗杆的高度，移动竹竿，使竹竿、旗杆顶端的影子恰好落在地面的同一点．此时，竹竿与这一点相距8m、与旗杆相距22m，则旗杆的高为（ ）

A．12m

B．10m

C．8m

D．7m

如图，△ABC中，点D、E分别是AB、AC的中点，则下列结论：①BC=2DE；②△ADE∽△ABC；③．其中正确的序号有      

阳光下，一根竹杆高6米，影长10米，同一时刻，房子的影长20米，则房子的高为           米．

如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．

（1）求线段CD的长；
（2）当t为何值时，△CPQ与△ABC相似？
（3）当t为何值时，△CPQ为等腰三角形？

如图，在一面与地面垂直的围墙的同侧有一根高10米的旗杆AB和一根高度未知的电线杆CD，它们都与地面垂直，为了测得电线杆的高度，一个小组的同学进行了如下测量：某一时刻，在太阳光照射下，旗杆落在围墙上的影子EF的长度为2米，落在地面上的影子BF的长为10米，而电线杆落在围墙上的影子GH的长度为3米，落在地面上的影子DH的长为5米，依据这些数据，该小组的同学计算出了电线杆的高度．

（1）该小组的同学在这里利用的是           投影的有关知识进行计算的；
（2）试计算出电线杆的高度，并写出计算的过程．

已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．

（1）画出△ABC向下平移4个单位长度得到的△A₁B₁C₁，点C₁的坐标是      ；
（2）以点B为位似中心，在网格内画出△A₂B₂C₂，使△A₂B₂C₂与△ABC位似，且位似比为2：1，点C₂的坐标是          ；
（3）△A₂B₂C₂的面积是              平方单位．

如图，△ABC中，DE∥BC，AD：DB=2：1，则△ADE与△ABC的面积之比是（ ）

A．4：1

B．8：1

C．4：9

D．2：3

如图1，矩形ABCD中，AB=4，AD=3，把矩形沿直线AC折叠，使点B落在点E处，AE交CD于点F，连接DE．

（1）求证：△DEC≌△EDA；
（2）求DF的值；
（3）如图2，若P为线段EC上一动点，过点P作△AEC的内接矩形，使其顶点Q落在线段AE上，定点M、N落在线段AC上，当线段PE的长为何值时，矩形PQMN的面积最大？并求出其最大值．