自古以来,天空中壮丽璀璨的景象吸引了人们的注意,智慧的头脑开始探索宇宙的奥秘。到17世纪,牛顿成功地解释了天体运行的规律,时至今日,数千颗人造卫星绕地球在“设定”的轨道上运行,在天体的运动中万有引力定律起到了决定性的作用。则有关下列说法正确的是:
| A.“地心说”认为地球是宇宙的中心,是静止不动的,其代表人物是哥白尼 |
| B.牛顿发现了万有引力定律,并测出了万有引力常量G |
| C.人造地球卫星运行轨道平面的圆心一定是地球的球心 |
| D.同步卫星一定位于赤道正上方,但离开赤道面的高度可以任意选取 |
我国发射的“亚洲一号”地球同步通讯卫星的质量为1.2t,在某一确定的轨道上运行,下列说法中正确的是( )
| A.它可以定位在北京正上方太空,所以我国可以利用它进行电视转播 |
| B.它的轨道平面一定与赤道平面重合 |
| C.若要发射一颗质量为2.4t的地球同步通讯卫星,则该卫星的轨道半径将比“亚洲一号”卫星的轨道半径大 |
| D.若要发射一颗质量为2.4t的地球同步通讯卫星,则该卫星的线速度将比“亚洲一号”卫星的线速度小 |
发射地球同步通信卫星的基本方法是,先用火箭将卫星送入一近地椭圆轨道a运行,然后开动星载火箭变轨,将其送入与地球自转同步的轨道b,变轨点选在轨道a与轨道b内切的Q点,如图所示。下列说法正确的是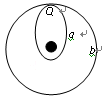



| A.卫星在Q点变轨时加速度变小 |
| B.卫星变轨后在Q点的机械能比变轨前的大 |
| C.卫星在轨道b运行速度小于在轨道a运行时的最小速度 |
| D.卫星在Q点变轨时星载火箭喷射气体的方向与卫星线速度方向相同 |
均匀分布在地球赤道平面上空的三颗同步通信卫星能够实现除地球南北极等少数地区外的“全球通信”。已知地球半径为R,地球表面重力加速度为g,地球自转周期为T,则三颗卫星中任意两颗卫星间的距离为:
A.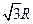 |
B. |
C.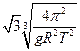 |
D.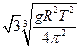 |
已知地球赤道上的物体随地球自转的线速度大小为 ,向心加速度大小为
,向心加速度大小为 ,近地卫星速度大小为
,近地卫星速度大小为 ,向心加速度大小为
,向心加速度大小为 ,地球同步卫星线速度大小为
,地球同步卫星线速度大小为 ,向心加速度大小为
,向心加速度大小为 ,设近地卫星距地面高度不计,同步卫星距地面高度约为地球半径的6倍,则以下结论正确的是( )
,设近地卫星距地面高度不计,同步卫星距地面高度约为地球半径的6倍,则以下结论正确的是( )
A. |
B. |
C. |
D. |
已知地球同步卫星的轨道半径是地球半径的 倍,则
倍,则
A.第一宇宙速度是同步卫星运行线速度的 倍 倍 |
B.第一宇宙速度是同步卫星运行线速度的 倍 倍 |
C.地球表面附近的重力加速度是同步卫星向心加速度的 倍 倍 |
D.地球表面附近的重力加速度是同步卫星向心加速度的 倍 倍 |
如图11所示,发射地球同步卫星时,可认为先将卫星发射至距地面高度为h1的圆形近地轨道上,在卫星经过A点时点火(喷气发动机工作)实施变轨进入椭圆轨道,椭圆轨道的近地点为A,远地点为B。在卫星沿椭圆轨道运动到B点(远地点B在同步轨道上)时再次点火实施变轨进入同步轨道,两次点火过程都使卫星沿切向方向加速,并且点火时间很短。已知同步卫星的运动周期为T,地球的半径的R,地球表面重力加速度为g,求:
(1)卫星在近地圆形轨道运动时的加速度大小;
(2)同步卫星轨道距地面的高度.
如图甲所示,a是地球赤道上的一点,某时刻在a的正上方有b、c、d三颗轨道位于赤道平面的卫星,各卫星的运行方向均与地球自转方向(顺时针转动)相同,其中d是地球同步卫星。从此时刻起,经过时间t(已知 时间t均小于三颗卫星的运行周期),在乙图中各卫星相对a的位置最接近实际的是
时间t均小于三颗卫星的运行周期),在乙图中各卫星相对a的位置最接近实际的是
(8分) 已知地球的半径为R,自转角速度为 ,地球表面的重力加速度为g,在赤道上空一颗相对地球静止的同步卫星离地面的高度h是多少?(用以上三个量表示)
,地球表面的重力加速度为g,在赤道上空一颗相对地球静止的同步卫星离地面的高度h是多少?(用以上三个量表示)
(1)求卫星B的运行周期
(2)如卫星B绕行方向与地球自转方向相同,某时刻A、B两卫星相距最近(O、B、A在同一直线上),则至少经过多长时间,他们再一次相距最近?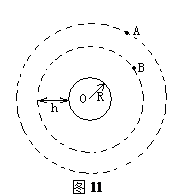
同步卫星是指相对于地面不动的人造地球卫星,则下面说法中正确的是( )
| A.它可以在地面上任一点的正上方,且离地心的距离可按需要选择不同的数值 |
B.它可以在地面上任一点的正上方,但离地心的距离是一定的 |
C.它只能在赤道的正上方,但离地心的距离可按需要选择不同的数值 |
D.它只能在赤道的正上方,且离地心的距离是一定的 |
一地球卫星高度等于地球半径,用弹簧秤将一物体悬挂在卫星内,物体在地球表面时,重力为98N,则它在卫星中受地球的引力为________N,物体的质量为________kg,弹簧秤的读数为_________N.