如图，已知:在平面直角坐标系中，四边形 是长方形， 点与原点重合，坐标为 ．
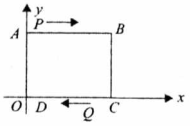
（1）写出点 的坐标;
（2）动点 从点 出发以每秒 个单位长度的速度向终点 运动，动点 从点 出发以每秒 个单位长度的速度沿射线 方向匀速运动，若 两点同时出发，设运动时间为 秒，当 为何值时， ?
（3）在点 的运动过程中，当点 运动到什么位置时，使 ?求出此时 点的坐标．
相关试题
如图，已知△ABC的三个顶点分别为A（2，3）、B（3，1）、C（－2，－2）。
（1）请在图中画出△ABC关于y轴的轴对称图形△DEF（A、B、C的对应点分别是D、E、F），并直写出D、E、F的坐标。
（2）求四边形ABED的面积。
；
已知：如图1，在△ABC中，A、B、C的坐标分别为（1,0），（4,0），（0,2），点M为边BC上的中点，点N为边AB 上一点，且N的横坐标为方程2n２＋5n－12＝0一个根，
（1）求N的坐标和直线MN的解析式 ；（3+3）
（2）判断直线MN与BC的位置关系，并说明你的理由；（1+3）
（3）如图2，①在图2中作出△ABC的外接圆；②过Q（
，0）作直线
⊥x轴，点P在直线上，且在第一象限，试确定一个点P，使得∠CPB+∠CAB=180°，求出满足条件的P点坐标．
粤公网安备 44130202000953号