已知正方形 中, 绕点 顺时针旋转,它的两边分别交 (或它们的延长线)于点 .当 绕点 旋转得到 时(如图1),易证 .
(1)当 绕点 旋转到 时(如图2),线段 和 之间有怎样的数量关系?写出猜想,并加以证明;
(2)当 绕点 旋转到如图3的位置时,线段 和 之间又有怎样的数量关系?写出你的猜想,并说明理由.
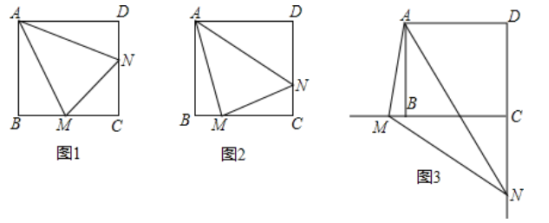
已知正方形 中, 绕点 顺时针旋转,它的两边分别交 (或它们的延长线)于点 .当 绕点 旋转得到 时(如图1),易证 .
(1)当 绕点 旋转到 时(如图2),线段 和 之间有怎样的数量关系?写出猜想,并加以证明;
(2)当 绕点 旋转到如图3的位置时,线段 和 之间又有怎样的数量关系?写出你的猜想,并说明理由.
