如图,已知正方形 ,点 是 边上一点,将 沿直线 折叠,点 落在 处,连接 并延长,与 的平分线相交于点 ,与 分别相交于点 , ,连接 .
(1)求证:
(2)若 ,求点 到直线 的距离;
(3)当点 在 边上(端点除外)运动时, 的大小是否变化?为什么?
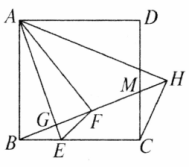
如图,已知正方形 ,点 是 边上一点,将 沿直线 折叠,点 落在 处,连接 并延长,与 的平分线相交于点 ,与 分别相交于点 , ,连接 .
(1)求证:
(2)若 ,求点 到直线 的距离;
(3)当点 在 边上(端点除外)运动时, 的大小是否变化?为什么?
