如图,在平面直角坐标系中,一次函数 的图象与 轴交于点 ,与 轴交于点 ,与直线 交于点.
(1)求直线 的函数表达式;
(2)过点 作 轴于点 ,将 沿射线 平移得到的三角形记为 ,点 的对应点分别为 ,若 与 重叠部分的面积为 ,平移的距离 ,当点 与点 重合时停止运动.
①若直线 交直线 于点 ,则线段 的长为______(用含有 的代数式表示);
②当 时, 与 的关系式为______;
③当 时, 的值为______.
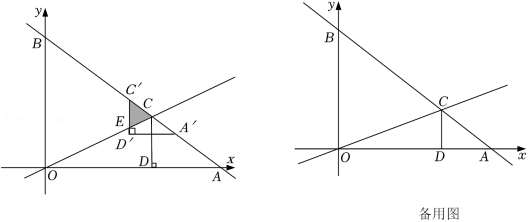
如图,在平面直角坐标系中,一次函数 的图象与 轴交于点 ,与 轴交于点 ,与直线 交于点.
(1)求直线 的函数表达式;
(2)过点 作 轴于点 ,将 沿射线 平移得到的三角形记为 ,点 的对应点分别为 ,若 与 重叠部分的面积为 ,平移的距离 ,当点 与点 重合时停止运动.
①若直线 交直线 于点 ,则线段 的长为______(用含有 的代数式表示);
②当 时, 与 的关系式为______;
③当 时, 的值为______.
