如图,四棱锥 P- ABCD的底面为正方形, PD⊥底面 ABCD.设平面 PAD与平面 PBC的交线为 l.
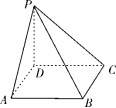
(1)证明: l⊥平面 PDC;
(2)已知 PD= AD=1, Q为 l上的点,求 PB与平面 QCD所成角的正弦值的最大值.
推荐套卷
如图,四棱锥 P- ABCD的底面为正方形, PD⊥底面 ABCD.设平面 PAD与平面 PBC的交线为 l.

(1)证明: l⊥平面 PDC;
(2)已知 PD= AD=1, Q为 l上的点,求 PB与平面 QCD所成角的正弦值的最大值.