已知抛物线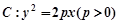 上有一点
上有一点 ,到焦点
,到焦点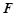 的距离为
的距离为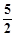 .
.
(Ⅰ)求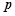 及
及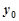 的值.
的值.
(Ⅱ)如图,设直线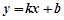 与抛物线交于两点
与抛物线交于两点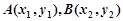 ,且
,且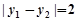 ,过弦
,过弦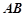 的中点
的中点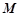 作垂直于
作垂直于 轴的直线与抛物线交于点
轴的直线与抛物线交于点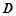 ,连接
,连接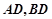 .试判断
.试判断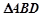 的面积是否为定值?若是,求出定值;否则,请说明理由.
的面积是否为定值?若是,求出定值;否则,请说明理由.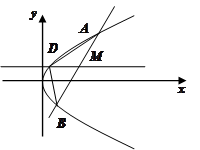
相关知识点
推荐套卷
已知抛物线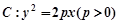 上有一点
上有一点 ,到焦点
,到焦点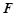 的距离为
的距离为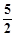 .
.
(Ⅰ)求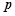 及
及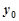 的值.
的值.
(Ⅱ)如图,设直线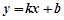 与抛物线交于两点
与抛物线交于两点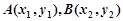 ,且
,且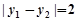 ,过弦
,过弦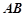 的中点
的中点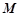 作垂直于
作垂直于 轴的直线与抛物线交于点
轴的直线与抛物线交于点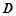 ,连接
,连接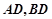 .试判断
.试判断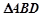 的面积是否为定值?若是,求出定值;否则,请说明理由.
的面积是否为定值?若是,求出定值;否则,请说明理由.