国庆节前,某超市为了满足人们的购物需求,计划购进甲、乙两种水果进行销售.经了解,甲种水果和乙种水果的进价与售价如下表所示.
甲 |
乙 |
|
进价(元/千克) |
x |
x+4 |
售价(元/千克) |
20 |
25 |
已知用1200元购进甲种水果的重量与用1500元购进乙种水果的重量相同.
(1)求x的值;
(2)若超市购进这两种水果共100千克,其中甲种水果的重量不低于乙种水果重量的3倍,则超市应如何进货才能获得最大利润,最大利润是多少?
推荐套卷
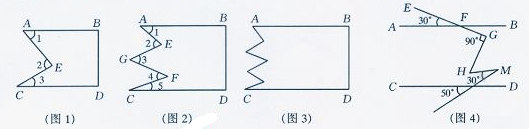
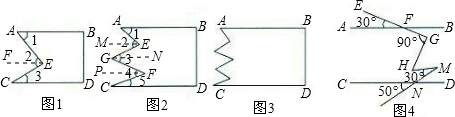
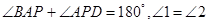 .试说明
.试说明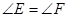 .
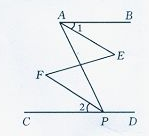
.

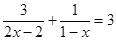
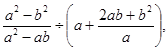 当
当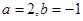 时,求代数式的值.
时,求代数式的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号