综合与探究
如图,抛物线 与 轴交于 , 两点(点 在点 的左侧),与 轴交于点 ,连接 , .
(1)求 、 , 三点的坐标并直接写出直线 , 的函数表达式.
(2)点 是直线 下方抛物线上的一个动点,过点 作 的平行线 ,交线段 于点 .
①试探究:在直线 上是否存在点 ,使得以点 , , , 为顶点的四边形为菱形,若存在,求出点 的坐标,若不存在,请说明理由;
②设抛物线的对称轴与直线 交于点 ,与直线 交于点 .当 时,请直接写出 的长.

相关知识点
推荐套卷
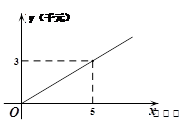
 的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数
的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数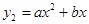 的图象如图②所示.
的图象如图②所示.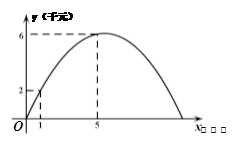
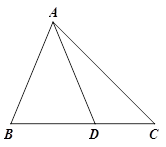
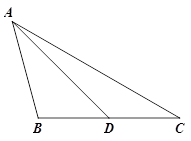
 交AC于点E,F是
交AC于点E,F是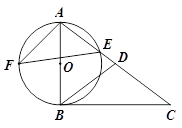
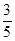 ,AE=
,AE=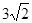 ,求sinF的值和AF的长.
,求sinF的值和AF的长. 粤公网安备 44130202000953号
粤公网安备 44130202000953号