根据对北京市相关的市场物价调研,预计进入夏季后的某一段时间,某批发市场内的
甲种蔬菜的销售利润y1(千元)与进货量x(吨)之间的函数 的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数
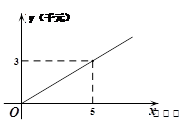
的图象如图①所示,乙种蔬菜的销售利润y2(千元)与进货量x(吨)之间的函数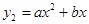 的图象如图②所示.
的图象如图②所示.
(1)分别求出y1、y2与x之间的函数关系式;
(2)如果该市场准备进甲、乙两种蔬菜共10吨,设乙种蔬菜的进货量为t吨,写出这两种蔬菜所获得的销售利润之和W(千元)与t(吨)之间的函数关系式,并求出这两种蔬菜各进多少吨时获得的销售利润之和最大,最大利润是多少?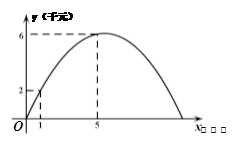
相关知识点
推荐套卷




 △ACE;
△ACE;
 粤公网安备 44130202000953号
粤公网安备 44130202000953号