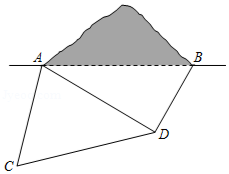
某工程队准备从 到 修建一条隧道,测量员在直线 的同一侧选定 , 两个观测点,如图.测得 长为 , 长为 , 长为 , , 、 、 、 在同一水平面内).
(1)求 、 两点之间的距离;
(2)求隧道 的长度.
相关知识点
推荐套卷
某工程队准备从 到 修建一条隧道,测量员在直线 的同一侧选定 , 两个观测点,如图.测得 长为 , 长为 , 长为 , , 、 、 、 在同一水平面内).
(1)求 、 两点之间的距离;
(2)求隧道 的长度.
