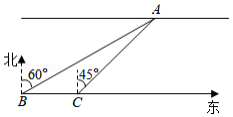
如图，一段河流自西向东，河岸笔直，且两岸平行．为测量其宽度，

首页 / 初中数学 / 试题详细

更新 2022-09-04
科目数学
题型解答题
难度中等
浏览 281

如图，一段河流自西向东，河岸笔直，且两岸平行．为测量其宽度，小明在南岸边 $B$ 处测得对岸边 $A$ 处一棵大树位于北偏东 $60 °$ 方向，他以 $1.5 m / s$ 的速度沿着河岸向东步行 $40 s$ 后到达 $C$ 处，此时测得大树位于北偏东 $45 °$ 方向，试计算此段河面的宽度（结果取整数，参考数据： $\sqrt{3} \approx 1.732)$

登录免费查看答案和解析

相关试题

如图，已知BC∥GE，AF∥DE，∠1=50°．

（1）求∠AFG的度数；
（2）若AQ平分∠FAC，交BC于点Q，且∠Q=15°，求∠ACB的度数．

题型：未知
难度：未知

收藏答案/解析

某校为了解九年级学生体育测试情况，以九年级（1）班学生的体育测试成绩为样本，按A，B，C，D四个等级进行统计，并将统计结果绘制成如下的统计图，请你结合图中所给信息解答下列问题：

（说明：A级：90分～100分；B级：75分～89分；C级：60分～74分；D级：60分以下）
（1）九年级（1）班体育测试的人数为；
（2）请把条形统计图补充完整；
（3）扇形统计图中A级所在的扇形的圆心角度数是；
（4）若该校九年级有500名学生，请你用此样本估计体育测试中A级和B级的学生人数约为多少人？