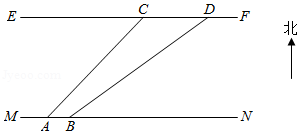
如图,线段 与 表示某一段河的两岸, .综合实践课上,同学们需要在河岸 上测量这段河的宽度 与 之间的距离),已知河对岸 上有建筑物 、 ,且 米,同学们首先在河岸 上选取点 处,用测角仪测得 建筑物位于 北偏东 方向,再沿河岸走20米到达 处,测得 建筑物位于 北偏东 方向,请你根据所测数据求出该段河的宽度,(用非特殊角的三角函数或根式表示即可)
相关知识点
推荐套卷
如图,线段 与 表示某一段河的两岸, .综合实践课上,同学们需要在河岸 上测量这段河的宽度 与 之间的距离),已知河对岸 上有建筑物 、 ,且 米,同学们首先在河岸 上选取点 处,用测角仪测得 建筑物位于 北偏东 方向,再沿河岸走20米到达 处,测得 建筑物位于 北偏东 方向,请你根据所测数据求出该段河的宽度,(用非特殊角的三角函数或根式表示即可)
