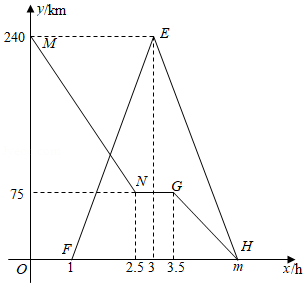
已知 、 两地相距 ，一辆货车从 前往 地，途中因装载货物停留一段时间．一辆轿车沿同一条公路从 地前往 地，到达 地后（在 地停留时间不计）立即原路原速返回．如图是两车距 地的距离 与货车行驶时间 之间的函数图象，结合图象回答下列问题：
（1）图中 的值是 ；轿车的速度是 ；
（2）求货车从 地前往 地的过程中，货车距 地的距离 与行驶时间 之间的函数关系式；
（3）直接写出轿车从 地到 地行驶过程中，轿车出发多长时间与货车相距 ？
如图，在△ABC，AB=AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CAB=2∠CBF．
（1）试判断直线BF与⊙O的位置关系，并说明理由；
（2）若AB=6，BF=8，求tan∠CBF．
如图，在一笔直的海岸线l上有A、B两个观测站，点A在点B的正东方向，AB=4km，有一艘小船在点P处，从点A 测得小船在北偏西60°方向，从点B测得小船在北偏东45°的方向．
（1）求小船到海岸线l的距离；
（2）小船从点P沿射线AP方向航行一段时间后，到C处，此时，从点B测得小船在北偏西15°的方向，求此时小船到观测点B的距离．（结果保留根号）
将如图所示的牌面数字分别是1，2，3，4的四张扑克牌背面朝上，洗匀后放在桌面上．
（1）从中随机抽出一张牌，牌面数字是偶数的概率是 ；
（2）从中随机抽出二张牌，两张牌牌面数字的和是5的概率是 ；
（3）先从中随机抽出一张牌，将牌面数字作为十位上的数字，然后将该牌放回并重新洗匀，再随机抽取一张，将牌面数字作为个位上的数字，请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率．
某体院要了解篮球专业学生投篮的命中率，对学生进行定点投篮测试，规定每人投篮20次，测试结束后随机抽查了一部分学生投中的次数，并分为五类，Ⅰ：投中11次；Ⅱ投中12次；Ⅲ：投中13次；Ⅳ：投中14次；Ⅴ：投中15次．根据调查结果绘制了下面尚不完整的统计图1、图2：
回答下列问题：
（1）本次抽查了 名学生，图2中的m= ．
（2）补全条形统计图，并指出中位数在哪一类．
（3）求最高的命中率及命中最高的人数所占的百分比．
（4）若体院规定篮球专业学生定点投篮命中率不低于65%记作合格，估计该院篮球专业210名学生中约有多少人不合格．
÷（a-
），再选取一个你喜欢的数a代入求值．
粤公网安备 44130202000953号