如图,在一笔直的海岸线l上有A、B两个观测站,点A在点B的正东方向,AB=4km,有一艘小船在点P处,从点A 测得小船在北偏西60°方向,从点B测得小船在北偏东45°的方向.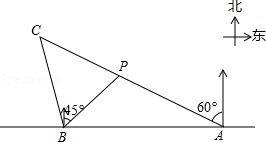
(1)求小船到海岸线l的距离;
(2)小船从点P沿射线AP方向航行一段时间后,到C处,此时,从点B测得小船在北偏西15°的方向,求此时小船到观测点B的距离.(结果保留根号)
相关知识点
推荐套卷
如图,在一笔直的海岸线l上有A、B两个观测站,点A在点B的正东方向,AB=4km,有一艘小船在点P处,从点A 测得小船在北偏西60°方向,从点B测得小船在北偏东45°的方向.
(1)求小船到海岸线l的距离;
(2)小船从点P沿射线AP方向航行一段时间后,到C处,此时,从点B测得小船在北偏西15°的方向,求此时小船到观测点B的距离.(结果保留根号)