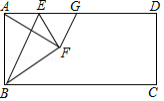
如图,在矩形 中,点 是 上的一个动点,连接 ,作点 关于 的对称点 ,且点 落在矩形 的内部,连接 , , ,过点 作 交 于点 ,设 .
(1)求证: ;
(2)当点 落在 上时,用含 的代数式表示 的值;
(3)若 ,且以点 , , 为顶点的三角形是直角三角形,求 的值.
相关知识点
推荐套卷
如图,在矩形 中,点 是 上的一个动点,连接 ,作点 关于 的对称点 ,且点 落在矩形 的内部,连接 , , ,过点 作 交 于点 ,设 .
(1)求证: ;
(2)当点 落在 上时,用含 的代数式表示 的值;
(3)若 ,且以点 , , 为顶点的三角形是直角三角形,求 的值.
