如图1,已知二次函数 、 、 为常数, 的图象过点 和点 ,函数图象最低点 的纵坐标为 ,直线 的解析式为 .
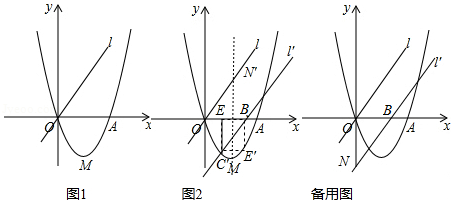
(1)求二次函数的解析式;
(2)直线 沿 轴向右平移,得直线 , 与线段 相交于点 ,与 轴下方的抛物线相交于点 ,过点 作 轴于点 ,把 沿直线 折叠,当点 恰好落在抛物线上点 时(图 ,求直线 的解析式;
(3)在(2)的条件下, 与 轴交于点 ,把 绕点 逆时针旋转 得到△ , 为 上的动点,当△ 为等腰三角形时,求符合条件的点 的坐标.
相关知识点
推荐套卷
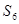 )拼成一个六边形,由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形,其面积可计算出为;由于所围成的小六边形的边长都是,其面积为,由此可得
)拼成一个六边形,由于大六边形三个角都是∠B+∠C=120°,所以由a边围成了一个大的正六边形,其面积可计算出为;由于所围成的小六边形的边长都是,其面积为,由此可得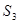 ),先画出这个正三角形,再推出
),先画出这个正三角形,再推出 边形吗?如果能,试写出∠A和三角形的面积
边形吗?如果能,试写出∠A和三角形的面积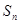 的表达式;如果不能,请简要说明理由.
的表达式;如果不能,请简要说明理由.
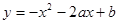 经过点A(1,0)和点P(3,4).
经过点A(1,0)和点P(3,4). 轴的另一个交点为B,现将抛物线向射线AP方向平移,使P点落在M点处,同时抛物线上的B点落在点D(BD∥PM)处.设抛物线平移前P、B之间的曲线部分与平移后M、D之间的曲线部分,与线段MP、BD所围成的面积为m, 线段 PM为n,求m与n的函数关系式.
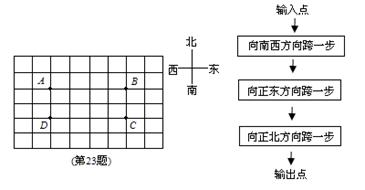
轴的另一个交点为B,现将抛物线向射线AP方向平移,使P点落在M点处,同时抛物线上的B点落在点D(BD∥PM)处.设抛物线平移前P、B之间的曲线部分与平移后M、D之间的曲线部分,与线段MP、BD所围成的面积为m, 线段 PM为n,求m与n的函数关系式.

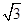 , ∠DPC=30°时,求⊙O的半径长.
, ∠DPC=30°时,求⊙O的半径长.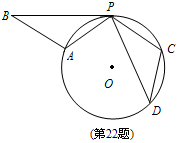
 粤公网安备 44130202000953号
粤公网安备 44130202000953号