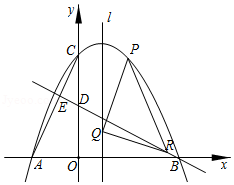
如图，已知抛物线 经过 ， ， 三点．
（1）求该抛物线的解析式；
（2）经过点 的直线交 轴于点 ，交线段 于点 ，若 ．
①求直线 的解析式；
②已知点 在该抛物线的对称轴 上，且纵坐标为1，点 是该抛物线上位于第一象限的动点，且在 右侧，点 是直线 上的动点，若 是以点 为直角顶点的等腰直角三角形，求点 的坐标．
（本小题满分9分）如图，抛物线y=x2+bx+c经过A（－1，0），B（4，5）两点，请解答下列问题：
（1）求抛物线的解析式；
（2）若抛物线的顶点为点D，对称轴所在的直线交x轴于点E，连接AD，点F为AD的中点，求出线段EF的长。注：抛物线y=ax2+bx+c的对称轴是x=
，顶点坐标是（
，
）。
（本小题满分10分）如图，在平面直角坐标系中，点A、B、C、P的坐标分别为（0，1）、（－1，0）、（1，0）、（－1，－1）。
（1）求经过A、B、C三点的抛物线的表达式；
（2）以P为位似中心，将△ABC放大，使得放大后的△A1B1C1与△OAB对应线段的比为3：1，请在右图网格中画出放大后的△A1B1C1；（所画△A1B1C1与△ABC在点P同侧）；
（3）经过A1、B1、C1三点的抛物线能否由（1）中的抛物线平移得到？请说明理由。
（本小题满分9分）深圳大运会期间，某宾馆有若干间住房，住宿记录提供了如下信息：①7月20日全部住满，一天住宿费收入为3600元；②7月21日有10间房空着，一天住宿费收入为2800元；③该宾馆每间房每天收费标准相同。（1）求该宾馆共有多少间住房，每间住房每天收费多少元？
（2）通过市场调查发现，每个住房每天的定价每增加10元，就会有一个房间空闲；己知该宾馆空闲房间每天每间费用10元，有游客居住房间每天每间再增加20元的其他费用，问房价定为多少元时，该宾馆一天的利润最大？
（本小题满分8分）在直角坐标系中，已知点A（－2，0）、B（0，4）、C（0，3），过点C作直线交x轴于点D，使得以D、O、C为顶点的三角形与△AOB相似，求点D的坐标。
粤公网安备 44130202000953号