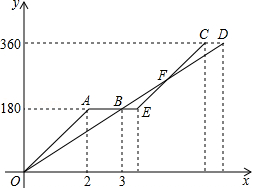
快车从甲地驶向乙地，慢车从乙地驶向甲地，两车同时出发并且在同一条公路上匀速行驶，途中快车休息1.5小时，慢车没有休息．设慢车行驶的时间为 小时，快车行驶的路程为 千米，慢车行驶的路程为 千米．如图中折线 表示 与 之间的函数关系，线段 表示 与 之间的函数关系．
请解答下列问题：
（1）求快车和慢车的速度；
（2）求图中线段 所表示的 与 之间的函数表达式；
（3）线段 与线段 相交于点 ，直接写出点 的坐标，并解释点 的实际意义．
相关试题
在一次测量中，小丽与欣欣利用温差来测量山峰的高度，小丽在山顶测得温度是–5℃ ，欣欣此时在山脚测得的温度是1℃ ，已知该地区高度每增加100米，气温大约降低0．8℃ ,则这个山峰的高度大约是多少米?
×
－（－
+（－
）÷
；
）+
－（
）
）
，23分别填在相应的大括号内．为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，该市自来水收费的收费标准如下表：
| 收费标准（注：水费按月份结算） |
|
| 每月用水量 |
单价（元/立方米） |
| 不超出6立方米的部分 |
2 |
| 超出6立方米不超出10立方米的部分 |
4 |
| 超出10立方米的部分 |
8 |
例如：某户居民1月份用水8立方米，应收水费为2×6+4×（8-6）=20（元）。
请根据上表的内容解答下列问题：
（1）若某户居民2月份用水5立方米，则应收水费多少元？
（2）若某户居民3月份交水费36元，则用水量为多少立方米？
（3）若某户居民4月份用水
立方米（其中6＜＜10），请用含的代数式表示应收水费．
（4）若某户居民5、6两个月共用水18立方米（6月份用水量超过了10立方米），设5月份用水
立方米，请用含的代数式表示该户居民5、6两个月共交水费多少元？
相关知识点
推荐套卷
粤公网安备 44130202000953号