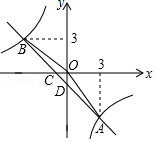
如图,一次函数 , 为常数, 的图象与反比例函数 的图象交于 、 两点,且与 轴交于点 ,与 轴交于点 , 点的横坐标与 点的纵坐标都是3.
(1)求一次函数的表达式;
(2)求 的面积;
(3)写出不等式 的解集.
相关知识点
推荐套卷
如图,一次函数 , 为常数, 的图象与反比例函数 的图象交于 、 两点,且与 轴交于点 ,与 轴交于点 , 点的横坐标与 点的纵坐标都是3.
(1)求一次函数的表达式;
(2)求 的面积;
(3)写出不等式 的解集.
